The conservation of ice mass equation becomes
η
η
υ
+υ
+η
= 0.
(113)
t
x
x
Expanding the terms in eq 110, combining with eq 112, and dividing by d, the con-
servation of water momentum equation becomes
η
d
u
u
+u
+g
+ gsi
- gSo
x
x
x
t
fbu2 (B + 2d)
u - υ
2
fi
B
(114)
1 +
+
= 0.
fb (B + 2d) u
8Bd
Similarly, after expansion of the partials in eq 111, combining with eq 113, and
dividing by η, the conservation of ice momentum equation becomes
υ
υ
η
η
+ g(1 - si )Kp (1 - p)
d
+υ
+ gsi
+g
t
x
x
x
x
g(1 - si )
(115)
f
k0λKp (1 - p)η - gSo - i (u - υ) = 0.
2
+
8si η
B
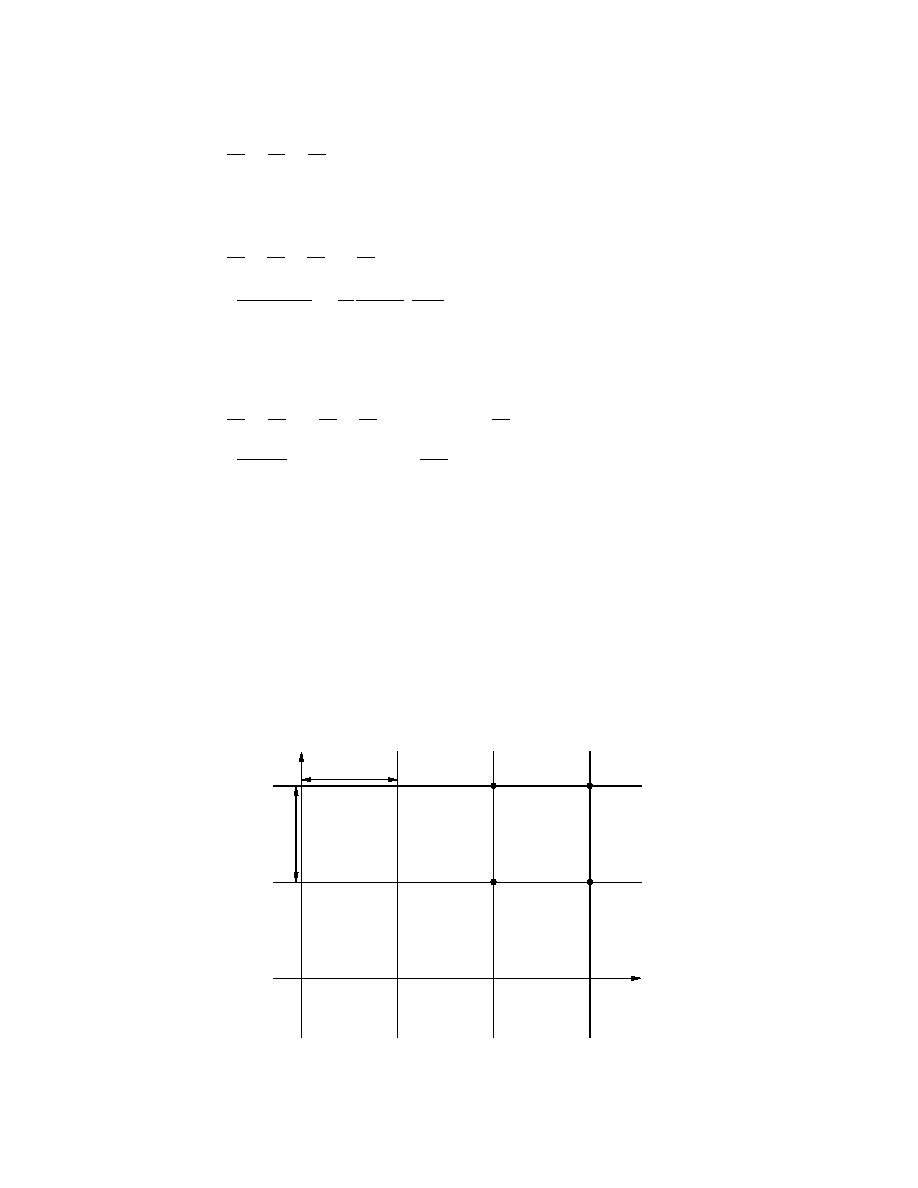
Figure 30 shows the computational grid used for the numerical simulations in
this study. The discretization of the governing equations assumes that the values of
the dependent variables and functions of the variables between the computational
grid points can be expressed in terms of the values at the grid points. A function
f(x,t) within the space interval j and (j + 1) is replaced by the following weighted
average
f (x, tn ) = Ψfjn1 + (1 - Ψ) fjn
(116a)
+
and
f (x, tn+1) = Ψfjn+1 + (1 - Ψ) fjn+1
(116b)
+1
t
∆x
t n+1
D(j, n+1)
C(j+1, n+1)
∆t
tn
A(j,n)
B(j+1, n)
t n1
x
xj
x j+1
x j1
Figure 30. Computational grid used for the numerical simulations.
44



 Previous Page
Previous Page
