[
]
(
) - (ρu A)
x2
t2
∫(
ρuA)t - (ρuA)t dx - ∫ ρu2 A
2
dt =
x2
t1
x1
2
1
x1
t2
t2 x2
g ∫ (ρI1)x - (ρI1)x dt + g ∫ ∫ ρ(A + Ai si )Sodxdt
2
t
1
t x
1
1 1
t2 x2
t2 x2
d
- g ∫ ∫ ρAi si So - dxdt - g ∫ ∫ ρASf dxdt.
x
(65)
t1 x1
t1 x1
If ρ is constant, eq 65 simplifies to
[
]
() ()
x2
t2
t2
dx - ∫ u2 A - u2 A dt = g ∫ (I1)x - (I1)x dt +
(uA)t 2 - (uA)t1
∫
2
t1
t1
x2
x1
1
x1
t2 x2
t2 x2
(66)
dxdt + g ∫ ∫ A(So - Sf ) dxdt.
d
g ∫ ∫ Ai si
x
t1 x1
t1 x1
Conservation of ice momentum
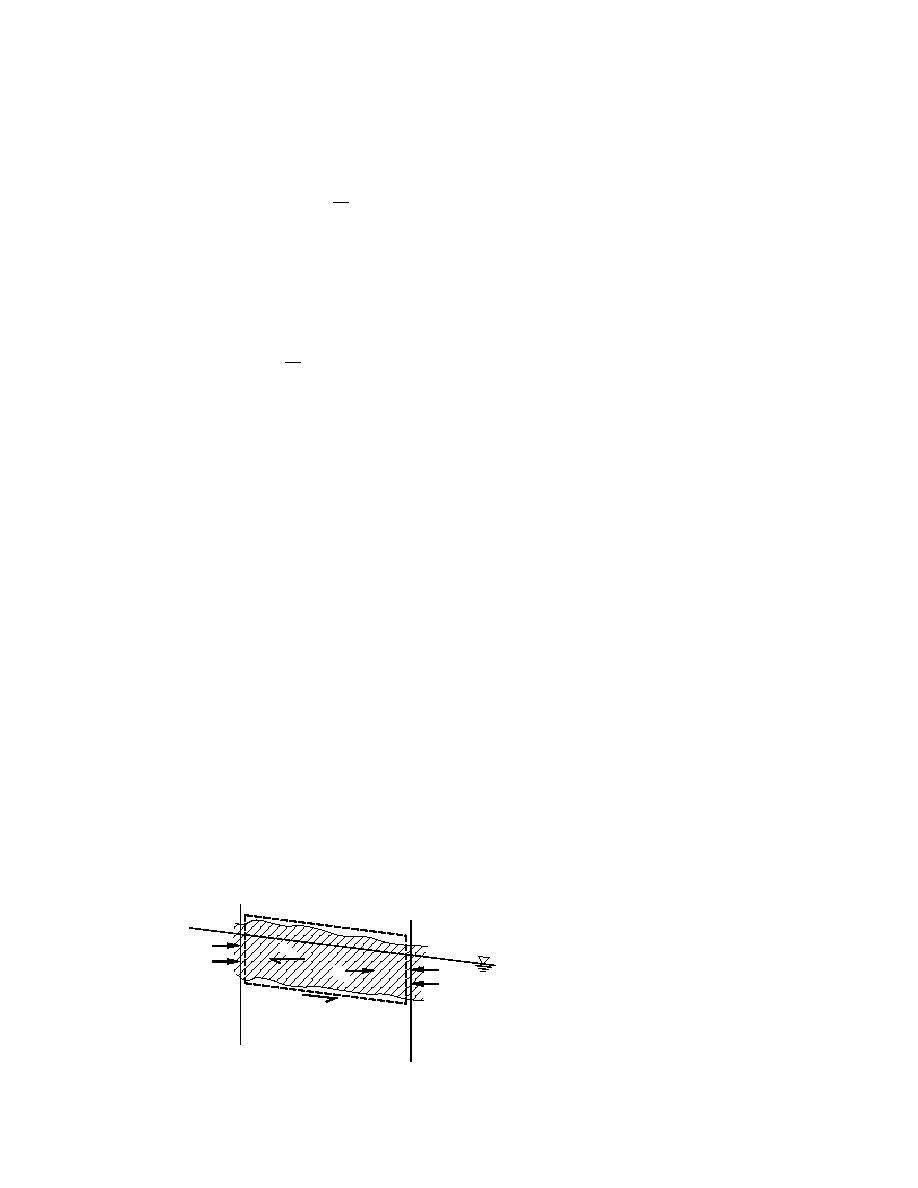
The ice control volume under analysis is bounded by x1, x2, and the bottom and
top of the jam. Figure 29 depicts the control volume and the forces acting on the
jam. The force associated with wind drag at the air/ice interface is neglected in this
formulation, though it could readily be included. The momentum of the ice and
pore water in the control volume at any instant is
x2
(
)
∫ ρi υAi [1 - p] + ρυAi si p dx.
(67)
x1
From ρi = siρ, and regrouping the p and (1 p) terms, the net increase in momentum
within the control volume between t1 and t2 becomes
x2
∆M = ∫ (siρυAi )t - (siρυAi )t dx.
1
(68)
x
2
1
The net momentum flux into the control volume is
[(ρ υ A [1 - p]) + (ρυ A s p)] - [(ρ υ A [1 - p]) + (ρυ A s p)]
2
2
2
2
.
(69)
i
i
ii
i
i
ii
x1
x2
Once again, from ρi = siρ, and regrouping the p and (1 p) terms, the net momen-
tum flux into the control volume between t1 and t2 becomes
(
) - (ρυ A s )
t2
Mf = ∫ ρυ2 Ai si
2
dt.
x2
(70)
ii
t1
x1
Fpp`
τxy
Fp2"
Fpp"
Fg3
Figure 29. Forces acting on the
Fp2"
ice control volume.
Ffi
x1
x2
37



 Previous Page
Previous Page
