As R = A/P, eq 58 can be rewritten as
αi fi Pi u - υ 2
α =
(59)
b fb Pb u
where αb and αi are the bed and ice-affected portions of the flow area. The total
shear stress is τb + τi and the total shear force on a unit length of channel is τbPb +
τ P + τi Pi
τ
τP
Sf =
=
= bb
.
(60)
ρgR ρgA
ρgA
The time integral of the friction force is
t2
t2 x2
t2 x2
∫ Ff dt = ∫ ∫ ρgASf dxdt = ∫ ∫ [τ bPb + τi Pi ] dxdt.
(61)
t1
t1 x1
t1 x1
Equations 55 to 57, rearranged in terms of the unknown variables u, υ, d, and η,
become
ρfbu2 Pb ρfi (u - υ) Pi
2
τ b Pb + τi Pi =
+
8
8
ρfbu2 Pb
fi (u - υ) Pi ρfbu2 Pb
2
αi
(62)
=
1 +
=
1 +
.
αb
fbu2 Pb
8
8
fi Pi u - υ 2
τ b Pb + τi Pi fbu2Pb
Sf =
=
1 +
.
(63)
fb Pb u
ρgA
8gA
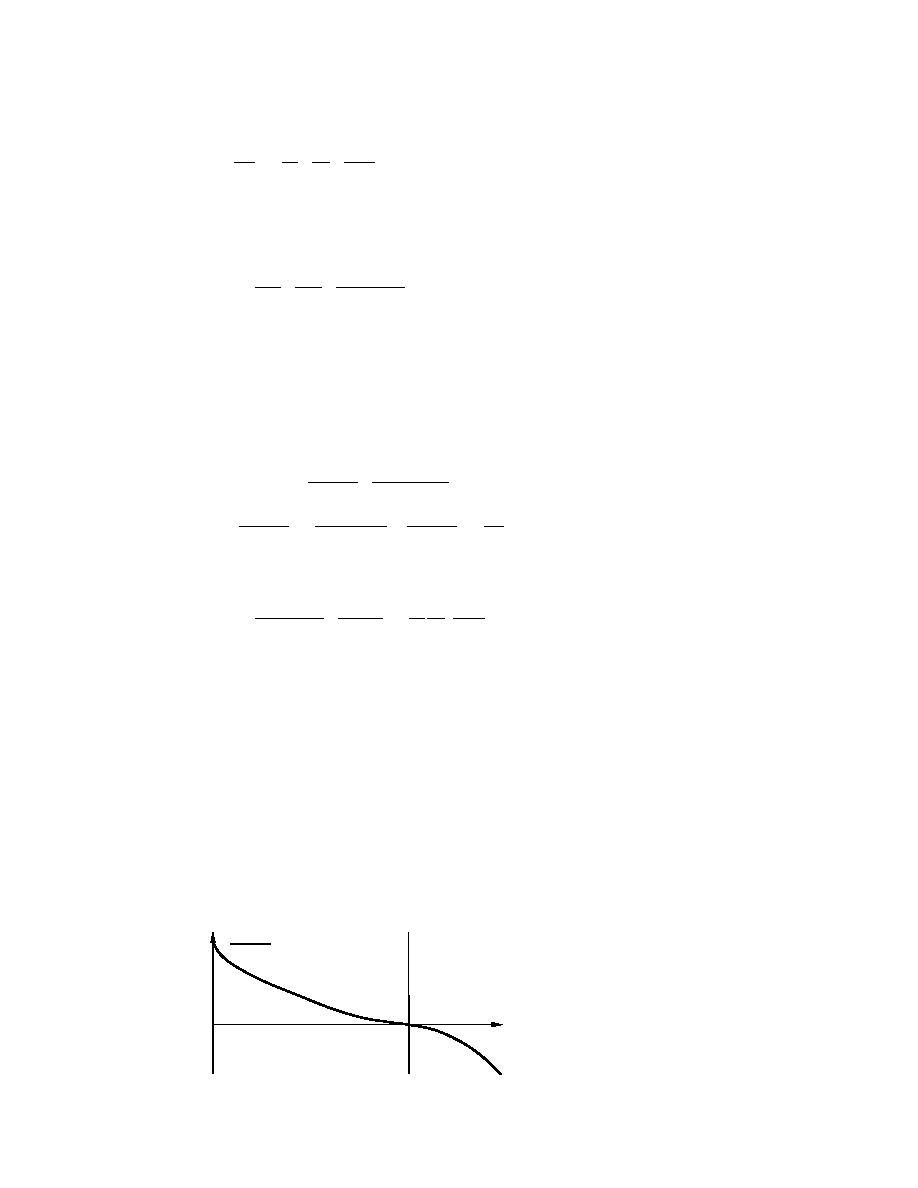
The effects of flow and ice velocities on τiPi are evident in Figure 28. As ice veloc-
ity increases beyond water velocity, the shear stress caused by the jam's presence
reverses to the downstream direction and the portion of the flow area affected by
this force increases.
The full momentum equation for the water flow can be written as
t2
t2
t2
t2
∆M - Mf = ∫ Fp1dt + ∫ Fg1dt - ∫ Fg2dt - ∫ Ff dt.
(64)
t1
t1
t1
t1
Equations 39, 40, 44, 48, 51, and 61 combined with eq 64 give
ρfiu2 Pi
υ=u
8
τi P
i
Figure 28. Shear force on the ice
jam underside vs. ice velocity
(τiPi vs. υ).
υ
36





 Previous Page
Previous Page
