Equation 2 shows that, as the length of the accumulation increases, the force
level reaches an asymptotic value that is related only to the water drag and cover
width (friction and lateral stress coefficients being constant). Kennedy's formula-
tion, however, neglected the streamwise component of the weight of the pulpwood
and assumed that the depth (and therefore water shear) was constant. Consequently,
the force through the jam would be independent of the thickness and bulk density
of the pulpwood accumulation.
Berdennikov (1964) investigated the forces exerted on an ice boom retaining an
ice accumulation. While he initially identified the weight component of the ice mass
parallel to the water surface as one of the forces to be considered, he dismissed this
force and the hydrodynamic pressure against the leading edge of the cover f1 as
being so small as to be negligible. His expression for the normal stress in the ice
field σx, assuming that σx = 0 at x = 0, is
Bτi
-2λk0x
σx =
1 - exp
.
B
(3)
2λk0η
Pariset and Hausser (1961), then Pariset et al. (1966), advanced Kennedy's for-
mulation by including the streamwise components of the weight of the cover and
an assumed "cohesive" stress acting between the ice and the banks. Summation of
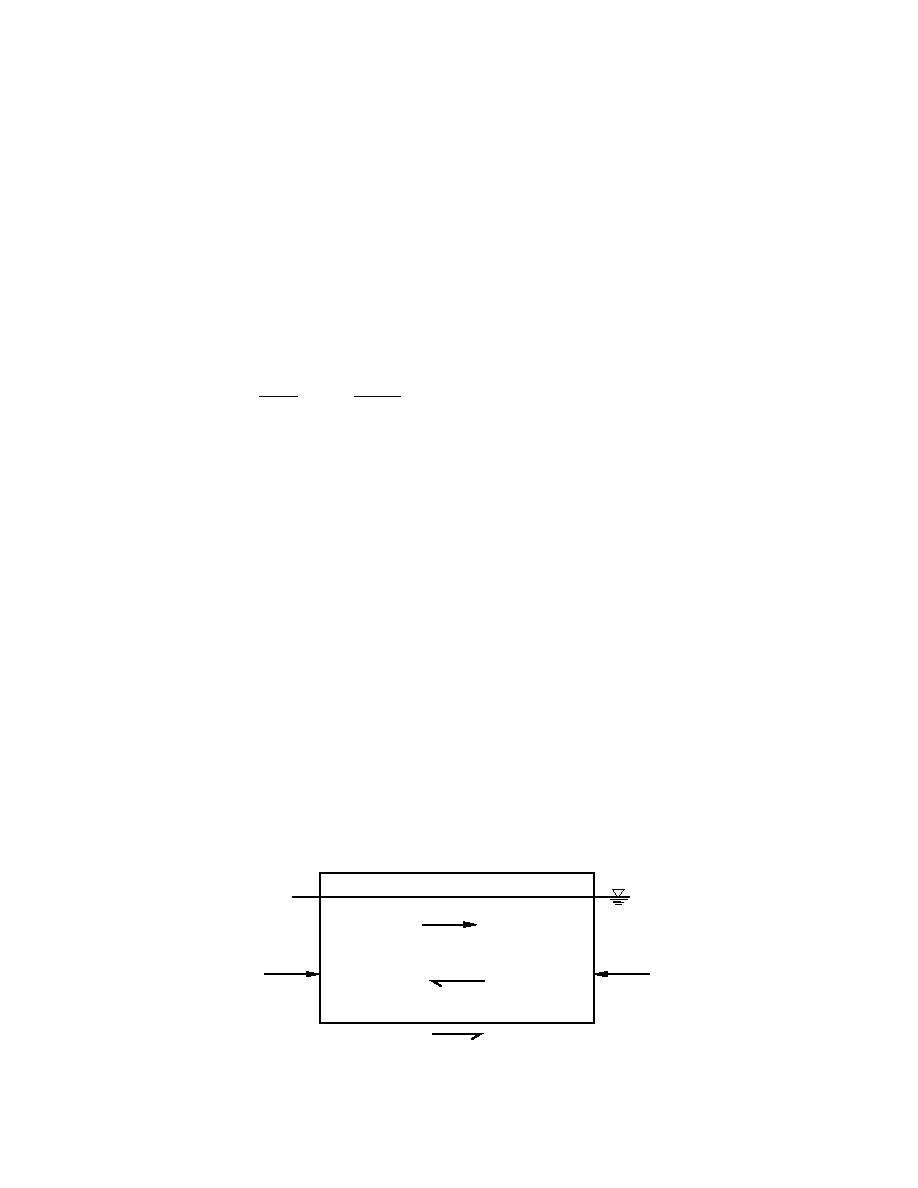
the forces acting on the ice cover (Fig. 13) gives
dFB + 2(τc η + λk0 F)dx = (τi + f3 )Bdx
(4)
where
F =
force per unit width acting in the downstream direction
τc =
cohesive stress per unit area at the banks
η =
cover thickness
f3 =
downstream component of the weight of the cover per unit area and B, k0,
λ, and τi are defined as above, so that
f3 = siρgηS
(5)
where
si =
specific gravity of ice
ρ =
density of water
g =
acceleration due to gravity
S =
slope.
f3
F+ F
F
(τ c η + k o λ F)
τi
Figure 13. Forces acting on an ice cover. (After Pariset et al. 1966.)
13



 Previous Page
Previous Page
