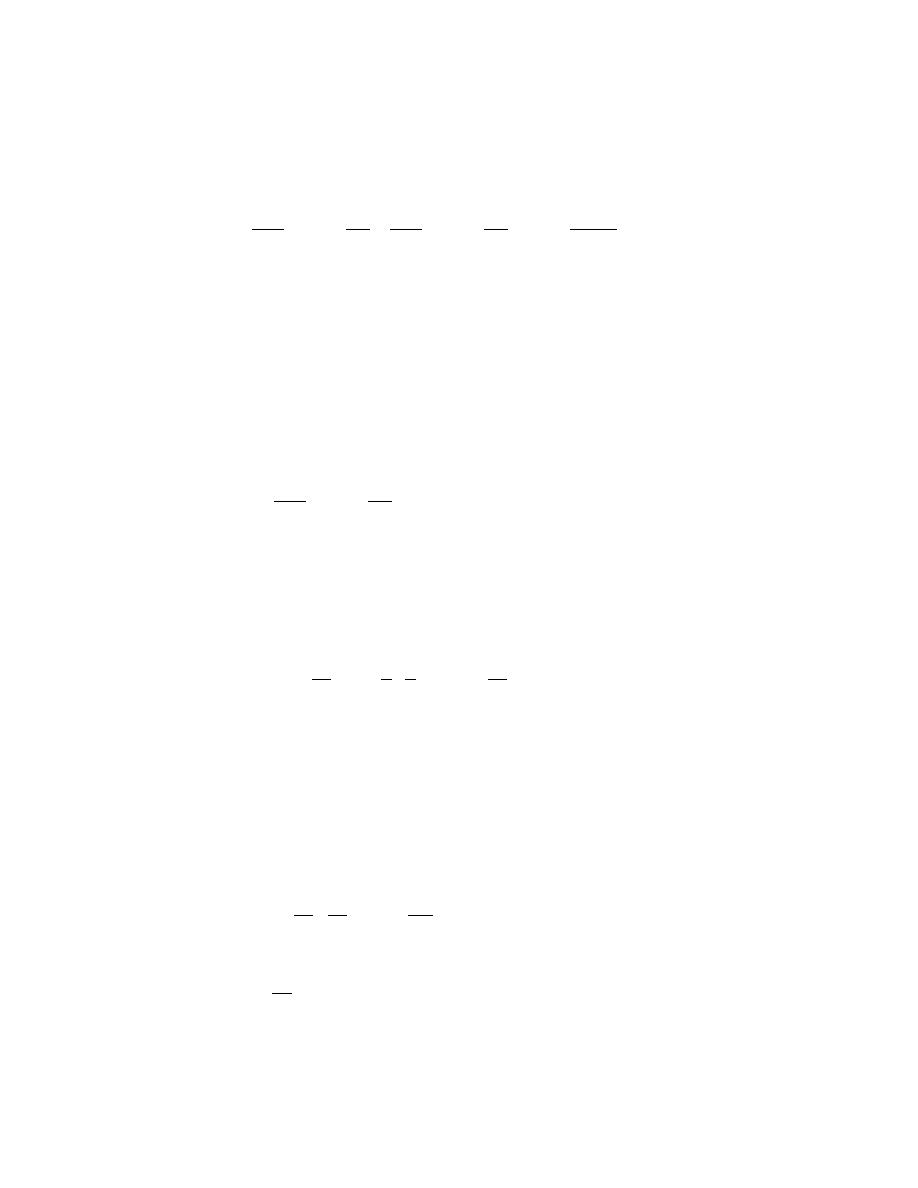
Because their formulation is for a uniform channel, bed slope, water surface slope,
and energy slope are taken as equal. Integration of eq 4 results in an expression for
the longitudinal force per unit width as a function of the distance from the
upstream edge of the cover, similar to eq 2, i.e.
τη B
τη
-2k0λx
(τi + f3 ) - kcλ - 2k λ (τi + f3 ) - kcλ - f1 exp B
B
F=
(6)
2k0λ
0
0
0
ness" of an ice jam over steady, uniform flow. Pariset et al. also suggest definitions
for narrow and wide jams. When the term within the large brackets of eq 6 (the
multiplier of the exponential term) is negative, the longitudinal force F is a maxi-
mum at the upstream edge of the cover (x = 0). This is the case for so-called narrow
jams. As the cover progresses upstream, the downstream thrust is resisted by shear
stress at the banks, which grows faster than the additional hydrodynamic forces
exerted on the jam. Conversely, when the term within the brackets is positive, the
longitudinal force F grows with distance downstream from the upstream edge of
the jam, asymptotically approaching a maximum as the distance grows very large.
This maximum longitudinal force acting through a wide jam is
τη
(τi + f3 ) - kcλ .
B
Fmax =
(7)
2k0λ
0
Pariset et al. recognized that this maximum force (or sum of external forces) is
resisted by the strength of the accumulated ice, which is assumed to behave as a
granular material. If Fmax exceeds jam strength, the jam fails and must thicken until
there is a balance between the external forces and jam strength. They likened the
maximum strength of the ice jam to that of a granular material under complete
mobilization of the passive pressure resistance, i.e.
η2
η2
2 π φ
Kpsiρg(1 - si )
= tan + siρg(1 - si )
(8)
4 2
2
2
the accumulated broken ice, and is commonly taken as the angle of repose for granu-
lar materials. Pariset et al. then equated jam internal stress to the sum of the stresses
exerted by the external forces. In doing so, they introduced the coefficient , where
= k0Kpλ
(9)
which combines the ice properties into one coefficient. The stress balance results in
an equation relating jam thickness and stresses exerted against the jam:
η2
τc η
(τi + f3 ) - .
B
siρg(1 - si )
=
(10)
2
2
The shear stress τi in eq 10 is expressible as
u2
τi = ρg 2
(11)
C
where u is water velocity beneath the cover and C is the Chezy coefficient. Pariset
et al. assumed that values of C are essentially equivalent for the ice surface and the
bed.
14





 Previous Page
Previous Page
