tribution from the seawater conductivity con-
tribution. A dual high and low frequency
0.74
νB = 584 σ
100
B
r 2 = 0.984
system or a wideband measurement system
S D = 3.169
could be used.
80
In the interim, an off-the-shelf electromag-
netic induction system operating at 10 kHz
60
can be used to estimate ice thickness (Fig. 8),
and the bulk salinity of the ice is estimated
using eq 2. After determining the average ice
40
sheet temperature, as previously described,
eq 1 can be used to calculate the bulk brine
20
volume. Ice strength may then be calculated
from eq 3 or 4.
The relation between sea-ice tensile or flex-
0
0.02
0.04
0.06
0.08
0.10
ural strength, brine volume, and the calcu-
σB , Bulk DC Conductivity (S/m)
lated bulk DC conductivity of natural sea ice
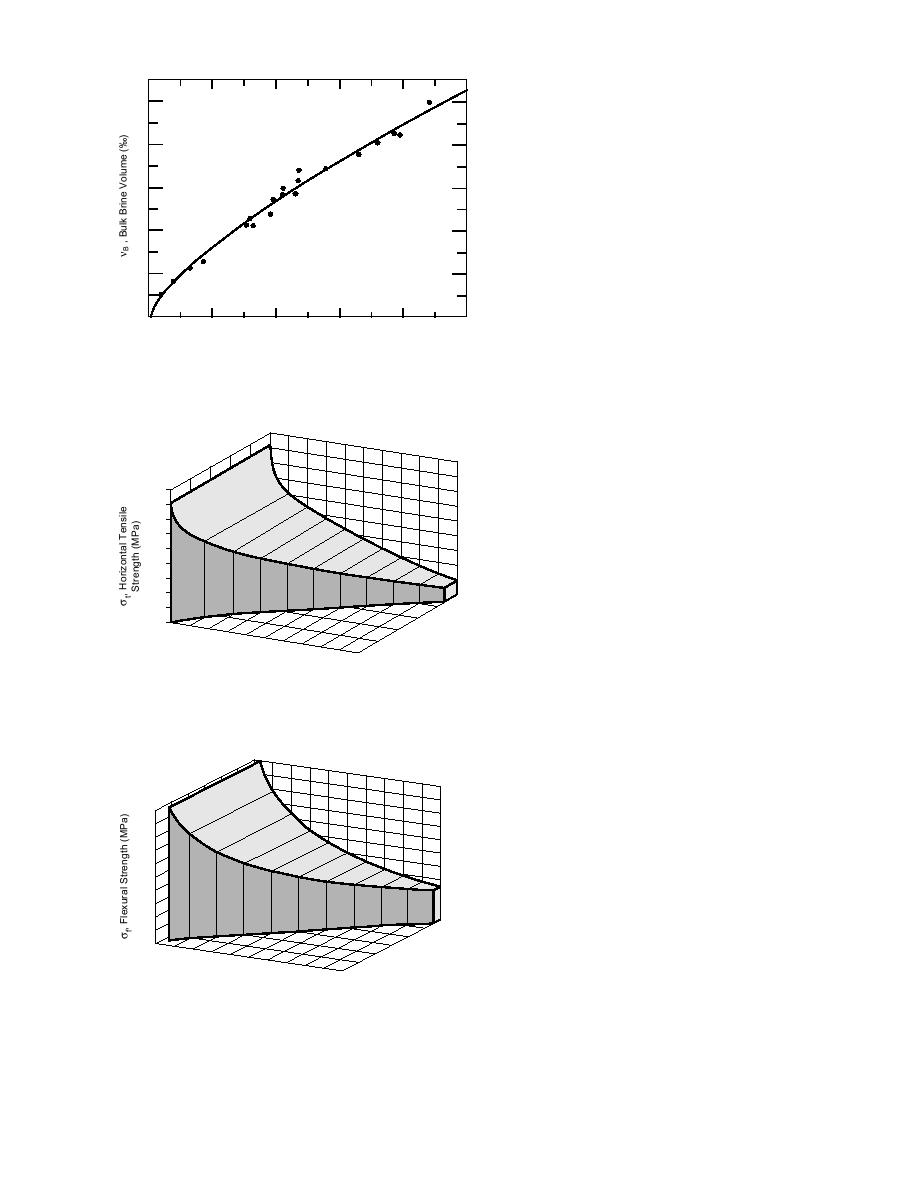
Figure 8. Measured sea-ice floe bulk brine volume vs. the
is shown in Figures 9 and 10. These figures
calculated bulk DC conductivity of the ice.
are the result of using the equation in Figure
6 and eq 3 and 4, respectively. In the future,
using similar equations, an algorithm
could be added to a portable electro-
magnetic induction sounding system
0.8
that would provide both ice thickness
and strength from the apparent sea-ice
0.8
0.6
conductivity measurements.
0.6
0.4
0.4
0.2
COMPRESSIVE STRENGTH
0.2
0
Estimating the compressive strength
100
‰)
e(
75
of sea ice is different. While the uniaxial
0
m
olu
50
eV
2
0.0
tensile or flexural strength of sea ice
.04
rin
25
.06
B
σ B, Bulk 0
ulk
.08
0
DC Con 0
does not reveal a significant strain rate
0
,B
ductivity 0
0.1
νB
(S/m)
dependence, at the strain rates of inter-
est for most ice engineering problems,
Figure 9. Ice sheet horizontal tensile strength vs. bulk DC
the compressive strength does. In addi-
conductivity and brine volume.
tion, in reporting sea-ice compression
test results, the recent, and correct,
method is to relate strength to total po-
rosity: brine volume plus gas volume.
1.0
Recently, Timco and Frederking (1990)
1.0
0.8
developed empirical equations for pre-
0.8
dicting the large-scale uniaxial uncon-
0.6
fined compressive strength of Arctic sea
0.6
0.4
ice. Their equations are based on small-
0.4
scale strength tests and the various con-
0.2
trolling factors, such as ice structure,
0.2
0
brine volume, porosity, loading direc-
100
‰)
(
80
me
0
tion (horizontalvertical), and strain
60
olu
eV
40
2
0.0
n
4
Bri
rate. Their strength equation for hori-
20
0.0
6
0.0
σ B, Bulk
ulk
8
0
0.0
0
B
0.1
ν B,
DC Con
zontally loaded columnar sea ice is
ductivity
(S/m)
[
],
σc = 37 ε0.22 1 - (φB / 270)
Figure 10. Ice sheet flexural strength vs. bulk DC conductiv-
0.5
˙
(5)
ity and brine volume.
6



 Previous Page
Previous Page
