processes, which reduce the vol-
0.93
0.10
+
ume fraction of the heavier brine
First-Year Ice +
ρB
σB
+
Multiyear Ice x
entrained within the ice (Kovacs
0.08
+
1996). The lower multiyear ice
0.92
+
densities are the result of this ice
+
containing proportionally less
0.06
0.91
brine and more gas, especially in
+
the freeboard portion, which is for
+
0.5
ρB = 0.9363 0.0018TF
+
++
0.04
all intents and purposes low-den-
+
r 2 = 0.919
+
+
0.90
S D = 0.002
sity fresh ice. While density is the
+ +
property that a material's strength
0.02
x
σ B = 0.147e
T /154
F
is often related to, as with the
r 2 = 0.915
x
0.89
strength of snow (Kovacs et al.
x
S D = 0.008
x
1969), it is not used for this pur-
0
pose in sea-ice mechanics. Tradi-
0.88
tionally, sea-ice failure strength,
0
200
400
600
800
TF , Floe Thickness (cm)
elastic modulus, and such have
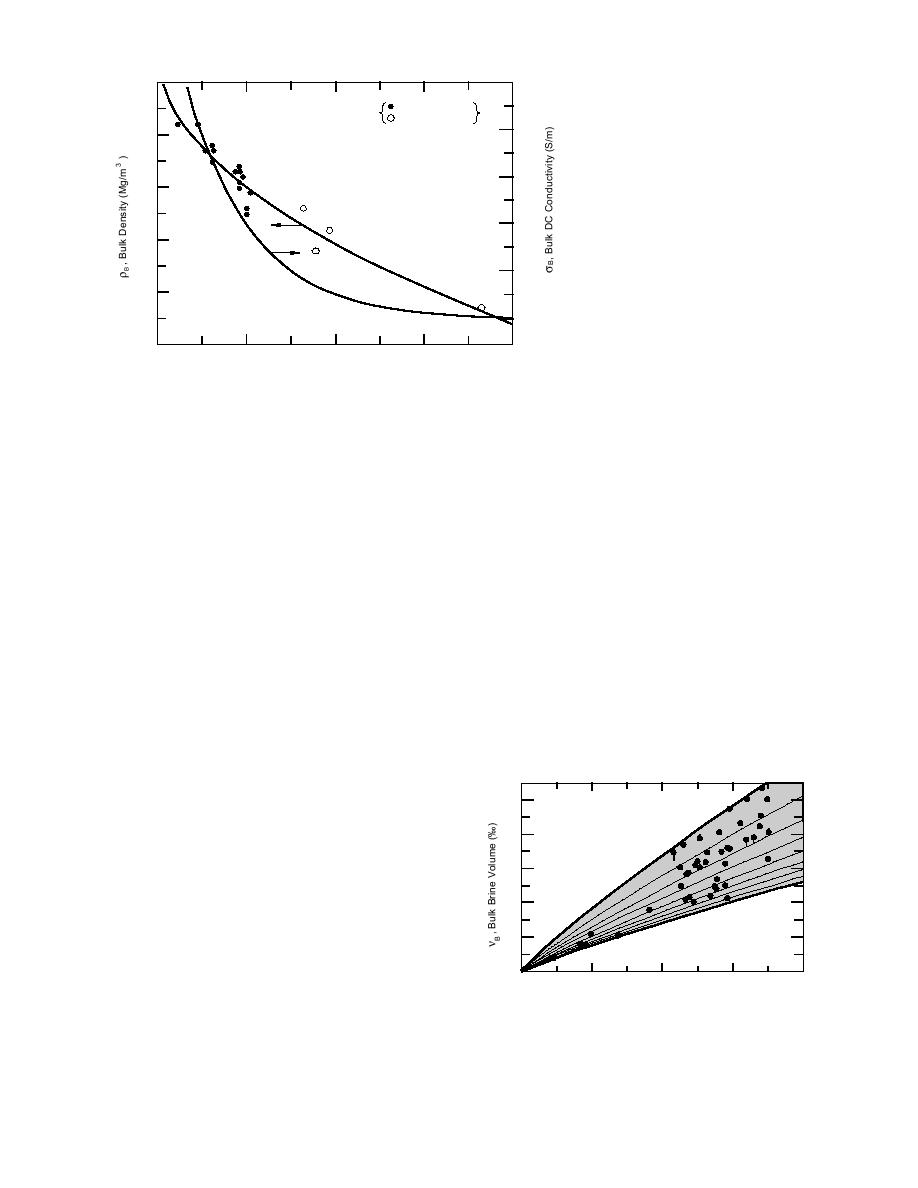
Figure 2. Sea-ice bulk density and conductivity vs. floe thickness.
been referenced to the brine vol-
ume of the ice. This brine volume
referencing is still the norm for sea-ice tensile or
brine-free ice density, the Frankenstein and Gar-
flexural strength test presentations. The reason-
ner (1967) equation also be used to estimate the
ing is that the strength of a material is a function
ice brine volume. When the two brine-volume
of its solidity. Therefore, the more brine volume
estimates are off by more than 2‰, a measure-
there is, the less solid the ice, and the weaker it
ment or data logging error has occurred. If the
will be. This method, of course, does not take into
problem cannot be resolved, the ice property val-
account the added porosity associated with the
ues calculated with the Cox and Weeks equations
small gas inclusions. Since brine volume, salinity,
should not be used. It should be noted that the
and temperature are interrelated, brine volume
Frankenstein and Garner equations for determin-
ing brine volume are not valid below 23C. Only
needs to be correlated with these two parameters,
as shown in Figure 3. This figure clearly illus-
the Cox and Weeks equations should be used
trates that, at any given bulk salinity SB, the bulk
below this temperature.
brine volume νB of an ice sheet is dependent on
The physical and electromagnetic properties of
21 winter Beaufort Sea ice cores, obtained by the
the average ice sheet temperature TA. While this
author on various field programs, were deter-
presentation is enlightening, it does not serve the
mined for each 10-cm increment of ice core. Physi-
user very well. More useful is the presentation in
cal property calculations were made using the
Figure 4, where the relationship provided allows
mathematical expressions of Cox and Weeks
for the determination of the bulk brine volume
(1983). The electromagnetic properties of the ice
were determined using the procedures of Kovacs
et al. (1987) as modified by Kovacs and Morey
100
(1987). Examples of the calculations are given in
Tables 1 and 2. Also assembled were the authors'
80
data from an additional 23 Beaufort Sea ice cores,
where only the salinity and temperature of the
3C
60
winter ice were determined for each 10-cm incre-
ment of core. For these data, only the brine vol-
40
ume of the ice could be calculated using the equa-
11C
tions of Frankenstein and Garner (1967).
20
From the above data, a number of winter ice
floe property trends can be seen. Ice floe bulk
0
8
2
4
6
density vs. thickness is shown in Figure 2. The
s B , Bulk Salinity (‰)
bulk density is seen to decrease with ice floe thick-
Figure 3. Sea-ice bulk brine volume vs. bulk salinity
ness. For the first-year sea ice, the decrease is
with average ice floe temperature as a parameter.
associated with brine drainage and growth rate
2




 Previous Page
Previous Page
