in eq 1 originate, respectively, from solutions to
4 1 d 2
Ea = + E
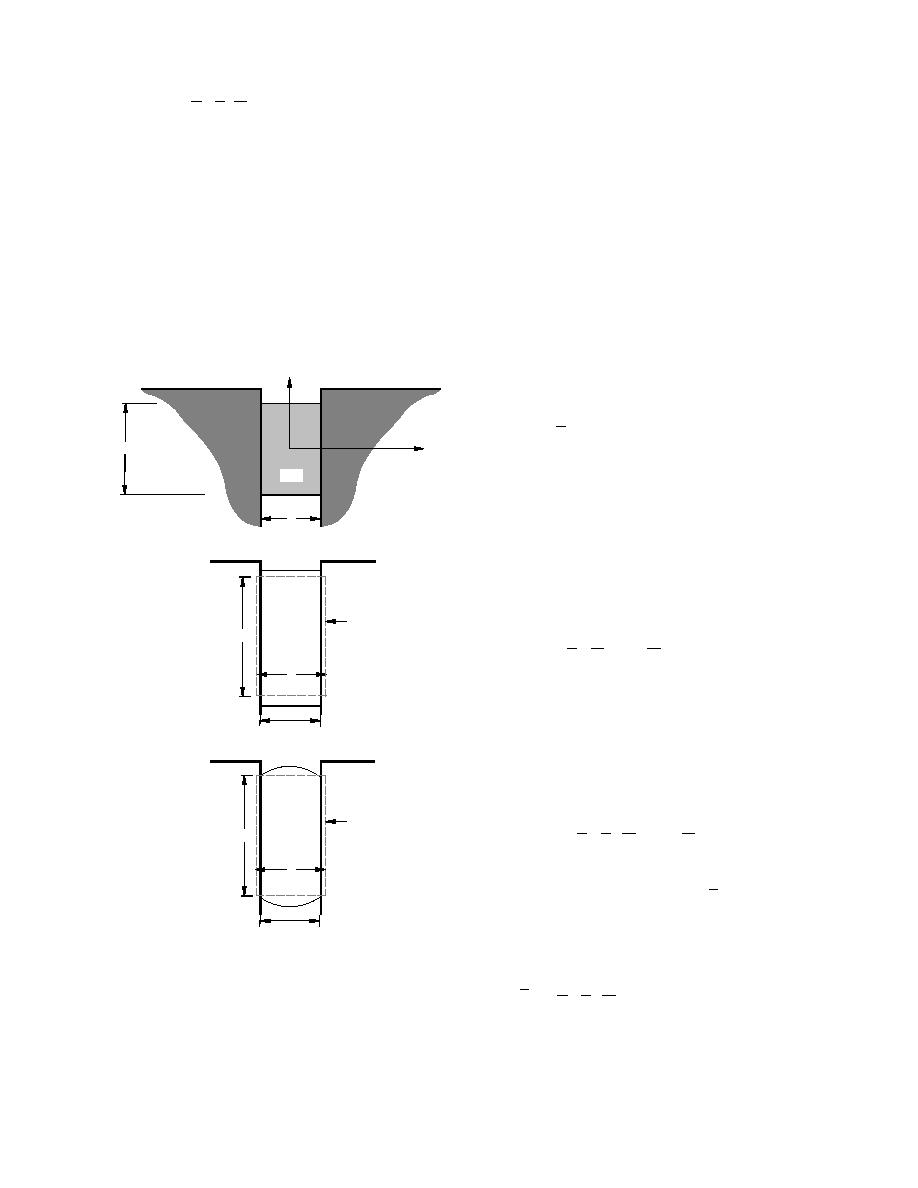
(a) a plane strain deformation in which the mate-
(1)
3 3 w
rial is free to slip on the bonded interface and to
deform homogeneously in the section, while re-
where E is the Young's modulus of the sealant,
maining constrained in the long direction, and (b)
and d and w are the depth and width of the seal
a subsequent inhomogeneous shear deformation
within the joint, respectively, as illustrated in Fig-
that restores the material of the bonded interface
ure 2a. In the literature of building and pavement
to the bonded position. These deformations are
seals, d/w is often called the shape factor of a seal.
depicted schematically in Figure 2, in parts b and
The term "apparent" was used by Gent and
c, respectively. The material is assumed to be in-
Lindley to distinguish the bonded extension or
compressible, i.e., it is assumed that there is no
compression deformation as an inhomogeneous
volume change during deformation. For the in-
structural deformation and to refer to the nomi-
homogeneous shear deformation, it is assumed
nal stress and strain of the structural response in
that planes parallel to the bonded surface remain
explicit contrast to the homogeneous stress and
plane, and that planes normal to these distort to
strain of a material property test. The two terms
form parabolas in the cross section. The solution
to the homogeneous deformation problem (a) is
y
the uniform normal stress, σx1, i.e.,
4
σx1 =
Ee
(2)
3
d
x
where e = ∆w/w is the joint extension or compres-
sion, i.e., the nominal strain of the seal, ∆w is the
Substrate
Seal
total joint movement in the x direction, and x
refers to the coordinate axis of Figure 2. The solu-
w
tion to the shear deformation problem (b) is a
a
hydrostatic pressure distribution, p(y), that varies
with the joint extension or compression, and along
the interface of the seal in the y direction, accord-
ing to
Undeformed
1 d 2
y
2
d
Configuration
()
p y = - 2 Ee
.
(3)
2 w
w
w
(See Chaloub and Kelly [1991] for an illustrative
derivation of the governing equation that p(y)
w + ∆w
satisfies.) A normal stress distribution, σx2 (y), is
b
in equilibrium with this pressure. The total nor-
mal stress distribution is found by the superposi-
tion of the stresses σx1 and σx2 (y), i.e.,
4 1 d 2
y
2
σx (y) = + - 2 Ee
Undeformed
d
(4)
Configuration
3 2 w
w
w
where σx is the total normal stress. The average of
this stress, i.e., the nominal stress σx , is found by
integrating σx (y) over the area d 1 of the inter-
w + ∆w
face and dividing by this area. The nominal stress
c
strain relation that follows is
Figure 2. (a) Original butt joint seal configuration,
4 1 d 2
(b) homogeneous deformation, and (c) final, inhomo-
σx = + Ee
3 3 w
geneous deformation, corresponding to solution of
(5)
Gent and Lindley (1959) for the compression of bonded
= Eae .
rubber blocks.
3



 Previous Page
Previous Page
