recast as follows
1/ 4
gρ (ρ - ρ ) k 3h
v l fg
h = 0.7071
.
(8)
ll
L (T - T ) θ dX
X
fb ∫0
l
sat
Substituting h from eq 8 in eq 1, the following integro-differential equation for θ is
obtained:
[
]
-1/ 4
d2θ
X
- Nθ
θ dX
=0
∫0
(9)
dX 2
where
gρl (ρl - ρv )kl hfgL7
1/ 4
3
N = 2.8284
.
(10)
lkf4D4
Equation 9 applies to both configurations of Figure 4, but the boundary conditions are
different. For the upward pointing fin, these are
dθ
X = 0,
= 0; X = 1, θ = 1 .
(11a,b)
dX
For the downward pointing fin, the boundary conditions are
dθ
X = 0,
θ = 1;
X = 1,
=0 .
(12a,b)
dX
Numerical solutions of eq 9 subject to boundary conditions (eq 11a,b or 12a,b) have
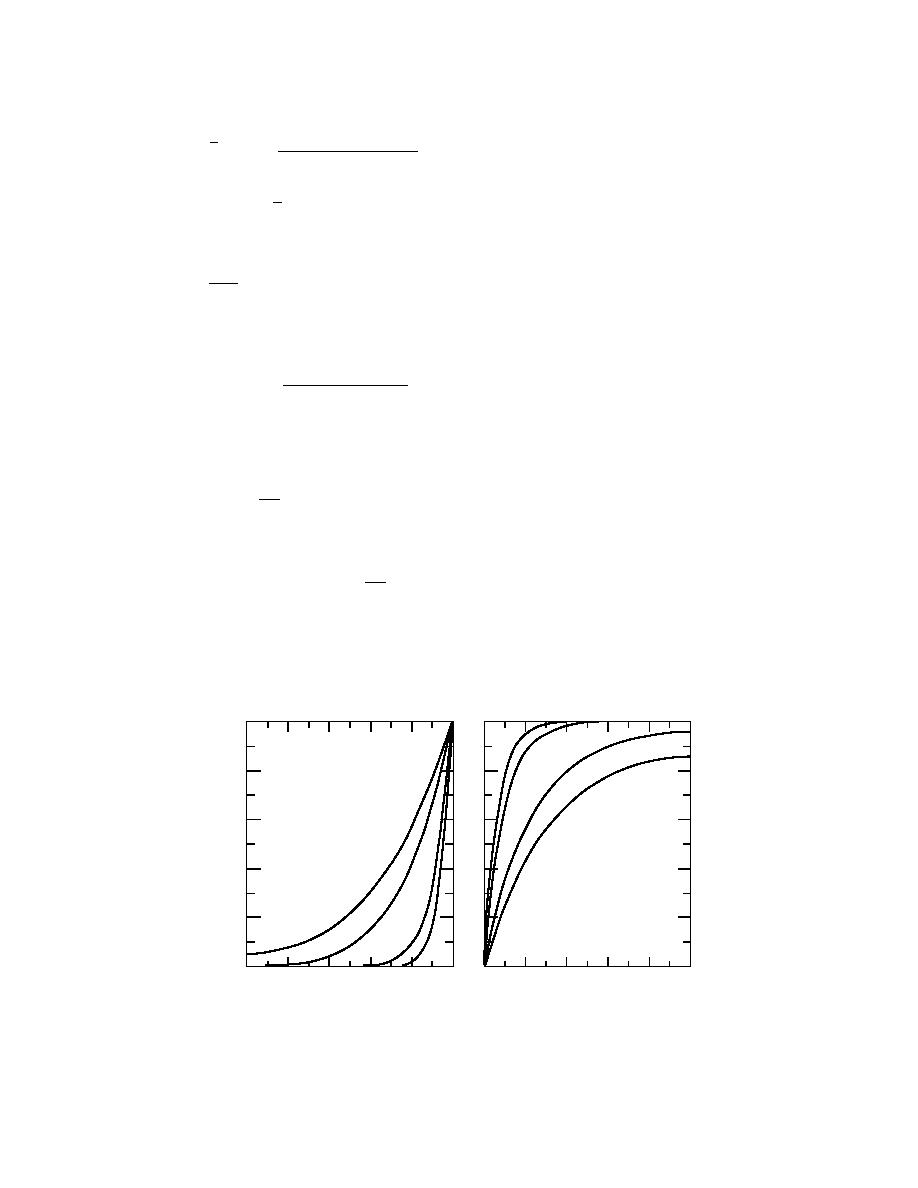
been reported by Lienhard and Dhir (1974). Figure 5 is an adaptation of their results. A
close examination of the left and the right portions of Figure 5 reveals that the tempera-
1.0
0
100
Upward
Pointing
50
0.2
0.8
10
N=5
0.4
0.6
θ
0.6
0.4
N=5
10
0.8
0.2
Downward
50
Pointing
100
1.0
0
0
0.2
0.4
0.6
0.8
1.0
0.2
0.4
0.6
0.8
1.0
X
X
Figure 5. Temperature distributions in vertical pin fins. Adapted from Lienhard
and Dhir (1974).
6




 Previous Page
Previous Page
