tion theory, and includes condensation of pure vapor as well as condensation of humid
air. Next, a section is devoted to the design of optimum fins for condensation applications.
The concluding part of the report refers briefly to vapor space condensation on horizontal
integral fin tubes, convective condensation in internally fined tubes, and condensation in
micro-fin tubes.
CONDENSATION ON SINGLE FINS
Nusselt-type models
The main difficulty in the analysis of film condensation on fins is the variability of the
heat transfer coefficient, h. Unlike the classical fin analysis that assumes h to be constant, h
for laminar condensation is a function of the difference between the local fin temperature
and the saturation of the condensing vapor. Another difficulty is that the surface (fin) is
nonisothermal, whereas the simple Nusselt theory applies to an isothermal surface. De-
spite these difficulties, it will be shown in the following subsections that a localized
application of Nusselt theory can be used at least for preliminary analysis and design.
Horizontal cylindrical (pin) fin
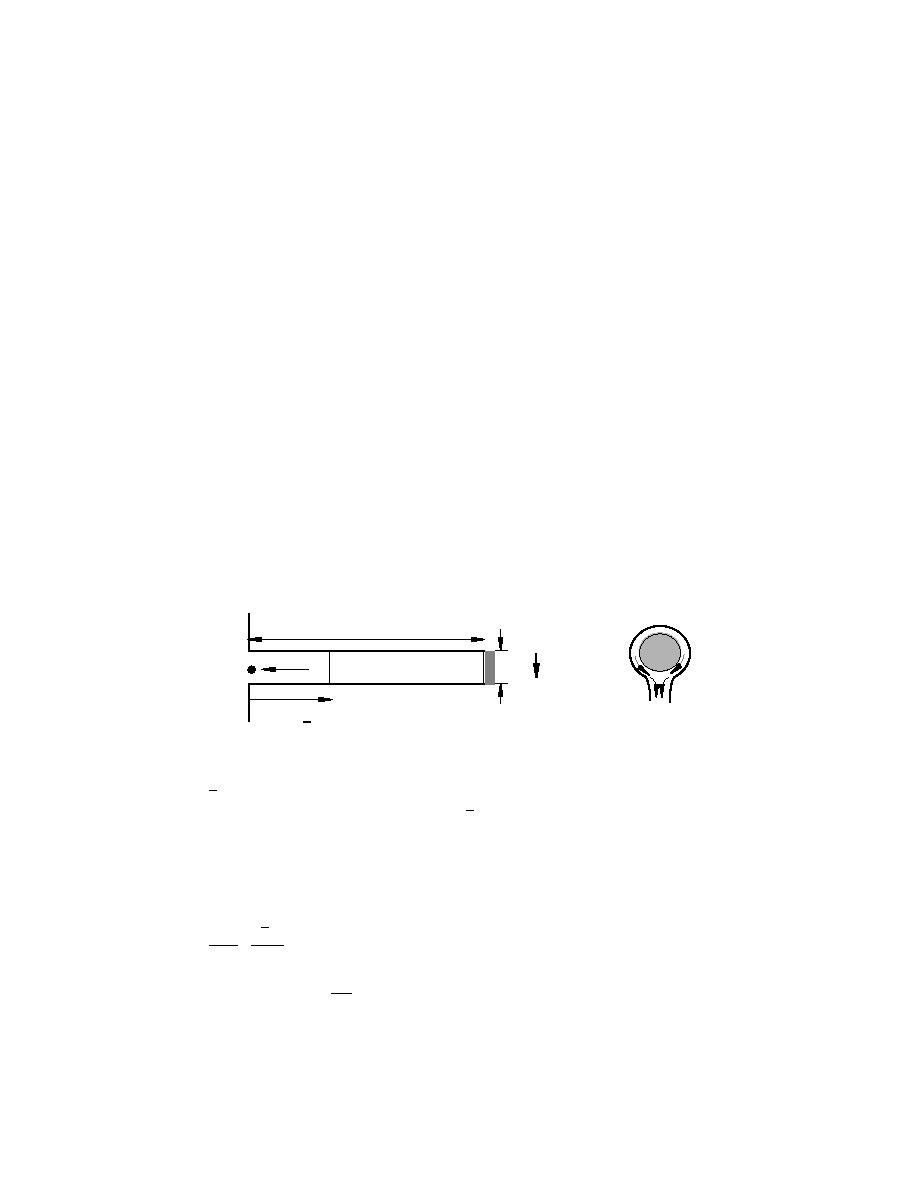
Consider a horizontal cylindrical fin of diameter D, length L, and thermal conductivity
kf as shown in Figure 1. The fin is in contact with a pure saturated, quiescent vapor at
temperature Tsat. The fin is attached to a cooled surface at fin base temperature Tfb (< Tsat).
Thus, the fin provides a cooled surface for the adjoining vapor to condense upon. Under
steady-state conditions, the latent heat extracted from the vapor is conducted into the
colder base. The condensate film formed on the surface of the fin drips down under the
action of gravity.
Saturated Vapor, Tsat
L
g
k f
Tfb
q
D
Condensate
Film
X
h (circumferential average)
Figure 1. Condensation on a horizontal pin fin.
axial location on the fin. Since the values of h are usually large, high values of the Biot
number Bi = hD/2k occur which, in turn, induce two-dimensional thermal effects in the
fin. We ignore this fact to avoid further complication, and assume that axial conduction is
the dominant mode of heat transfer through the fin. The equations governing the temper-
ature distribution in the fin can be written as
d2θ 4h L2
-
θ=0
(1)
dX 2
kf D
dθ
X = 0, θ = 1 ; X = 1,
=0
(2a,b)
dX
where θ = (Tsat - Tf )/(Tsat - Tfb ), X = x / L , and the boundary condition (eq 2b) implies an
2



 Previous Page
Previous Page
