insulated fin tip. To obtain h , we apply the Nusselt theory locally and use the well-known
expression for laminar condensation on a single, horizontal tube with zero interfacial
shear on the condensate film (Webb 1994). Thus, in terms of θ, we write
[
]
1/ 4
h = 0.728 gρl (ρl - ρv ) kl hfg / l (Tsat - Tfb ) θD
3
(3)
where g = acceleration due to gravity
ρl = density of condensate
ρv = density of vapor
l = absolute viscosity of the condensate
hfg = latent heat of condensation.
Substituting for h from eq 3 in eq 1 gives
d2θ
- Nθ3/ 4 = 0
(4)
2
dX
where the number of tubes on a fin is
[
]
1/ 4
N = 2.912 gρl (ρl - ρv ) kl hhgL8 /kf4 l (Tsat - Tfb ) D5
3
.
(5)
Since an analytical solution of eq 4 subject to boundary conditions (eq 2a,b) is not feasible,
a numerical procedure involving the combination of quasi-linearization and superposi-
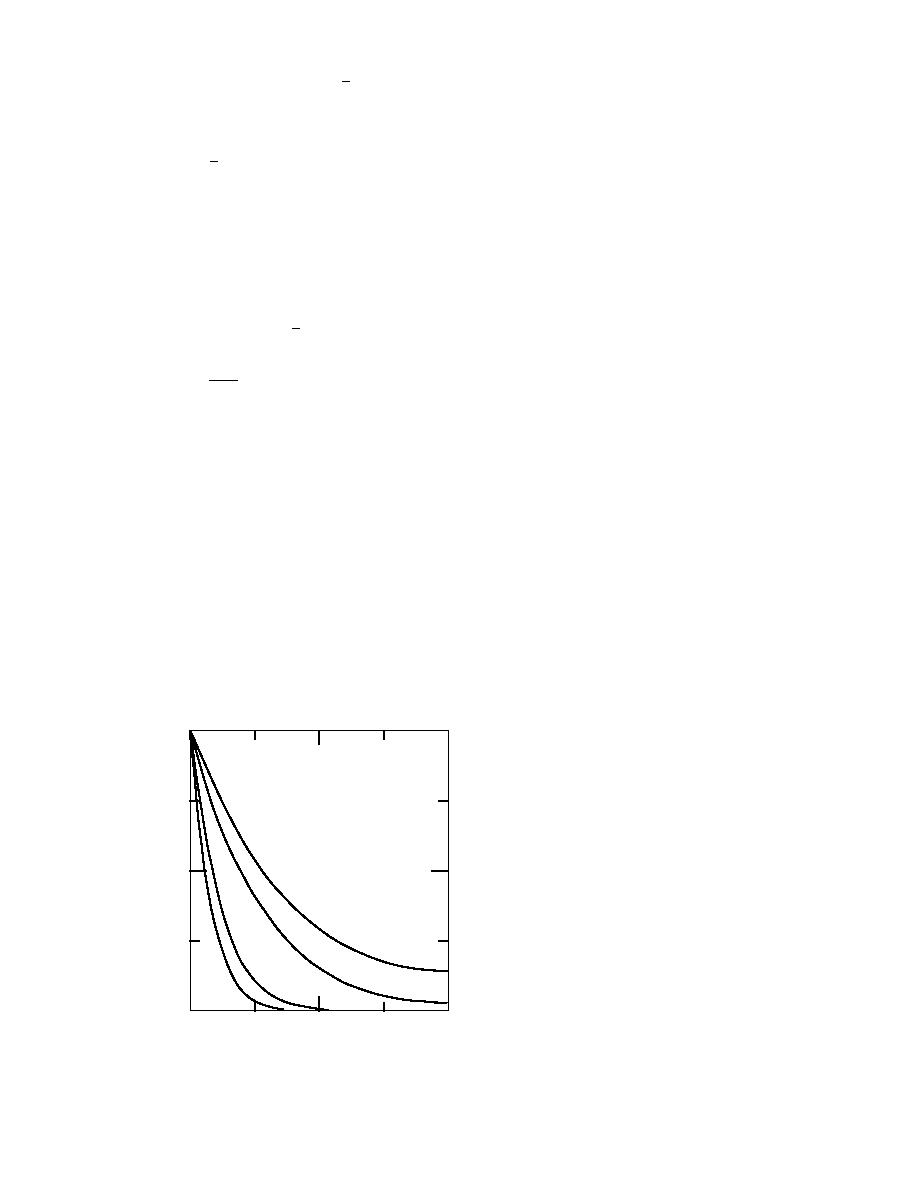
tion (Na 1979) was used to obtain the solution. Figure 2 displays the numerical results for
N = 5, 10, 50 and 100. These results match those of Lienhard and Dhir (1974) who used a
shooting method to generate the numerical solutions.
Figure 2 provides some insight into fin design. For N = 50 and 100, the last half of the fin
ly zero. Such a design is a waste of fin material. At low values of N, say N = 5, the
entire fin surface is effective in supporting condensation, but then the fin is too short for
substantial condensation augmentation. It is therefore reasonable to conclude that for
good design, N should be of the order of 10.
1.0
θ
0.5
N=5
10
50
100
Figure 2. Temperature distributions in a hor-
0
0.5
1.0
X
izontal pin fin with condensation.
3




 Previous Page
Previous Page
