80
Logarithmic Mean
Geometric Mean
60
Arithmetic Mean
40
20
0
0.2
0.4
0.6
0.8
1.0
Heat Load Ratio
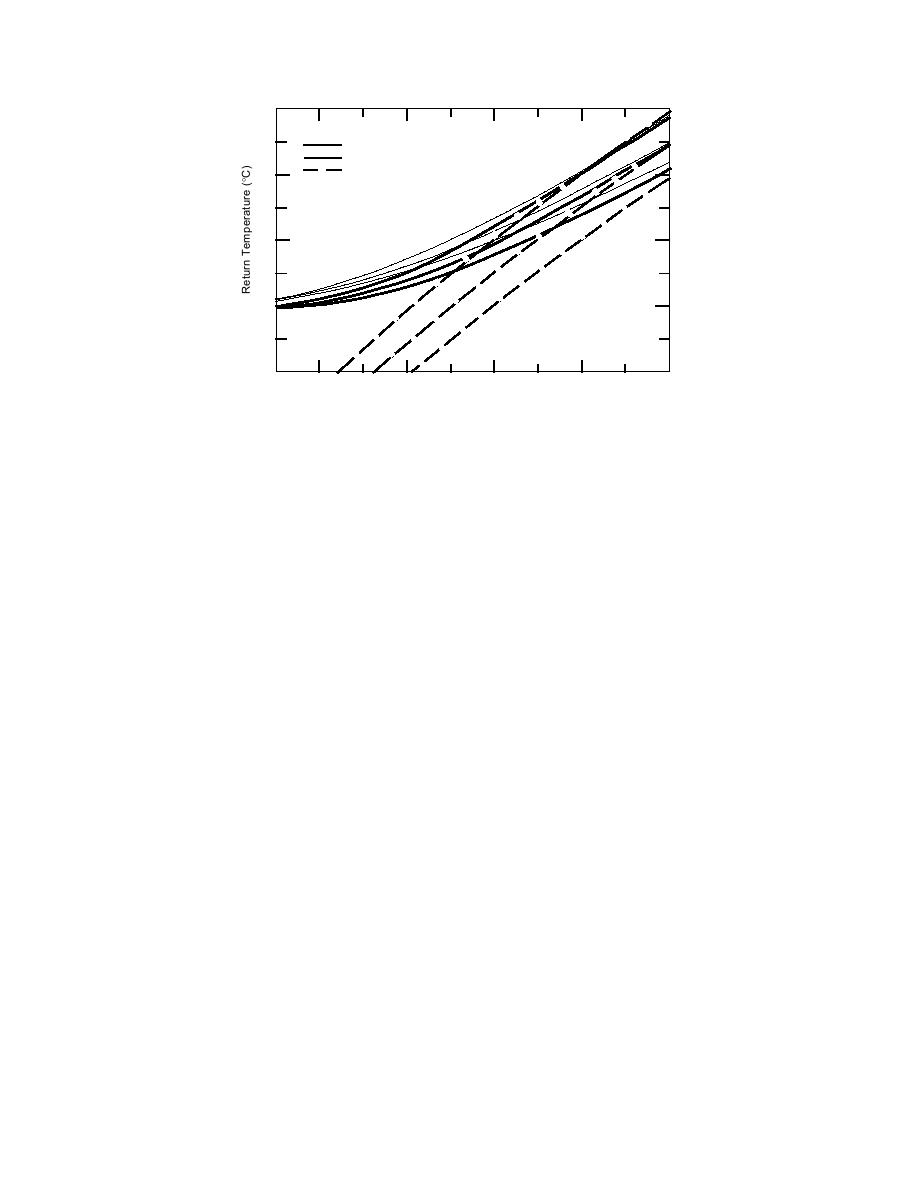
Figure 5. Results for the return temperature models. Top family is for Ts =
80C; middle family is for Ts = 90C; bottom family is for Ts = 100C.
by using the geometric mean approximation as an initial estimate, then proceeding
with a simple "iterative improvement" method where the previous estimate of (Tr)2
was substituted into the right-hand side of eq 3-19, which yielded the next estimate.
This procedure is repeated until successive estimates of (Tr)2 varied by no more than
the prescribed tolerance.
For each of the consumer models, we can easily develop an expression to calculate
the flow rate for any given load condition by starting with the heat balance for the
radiator. We assume that the mass of the radiator is negligible so that with the
gradual temperature changes typical of these systems, conditions are very close to
steady state. Treating the radiator as a control volume, we have
˙
q = m cp(Ts Tr)
(3-20)
where cp is the specific heat of water at constant pressure (kJ/kg C).
Thus, our mass flow rate relative to the mass flow rate at the design condition is
given by
˙
˙
m / m d = (q/qd)(Ts Tr)d/(Ts Tr)2.
(3-21)
Notice that we have used the d subscript to denote the design condition for the
piping system rather than the 0 subscript used to denote the design condition for the
consumer's radiators. If both the network piping and the consumer's radiators are
designed for the same maximum load condition, then it would not be necessary to
distinguish between these two conditions. However, in most cases this will not be
the case. For the piping network, little or no over-design is desirable in order to keep
costs at a minimum. In fact, diversity of demand between consumers will allow the
network to be designed for a total maximum demand of less than the sum of the
individual demands, as will be discussed later. The consumer's radiators, on the
other hand, will always be somewhat oversized. In addition to the normal conser-
vatism in design, quick recovery from night setback and other off periods also favors
significant over-design. Relative mass flow rates calculated using eq 3-21 for each of
the consumer models are given in Table 3. The results in Table 3 assume the same
design condition for the piping network and the consumer's radiators. Some
examples with differing design conditions will be given later.
25



 Previous Page
Previous Page
