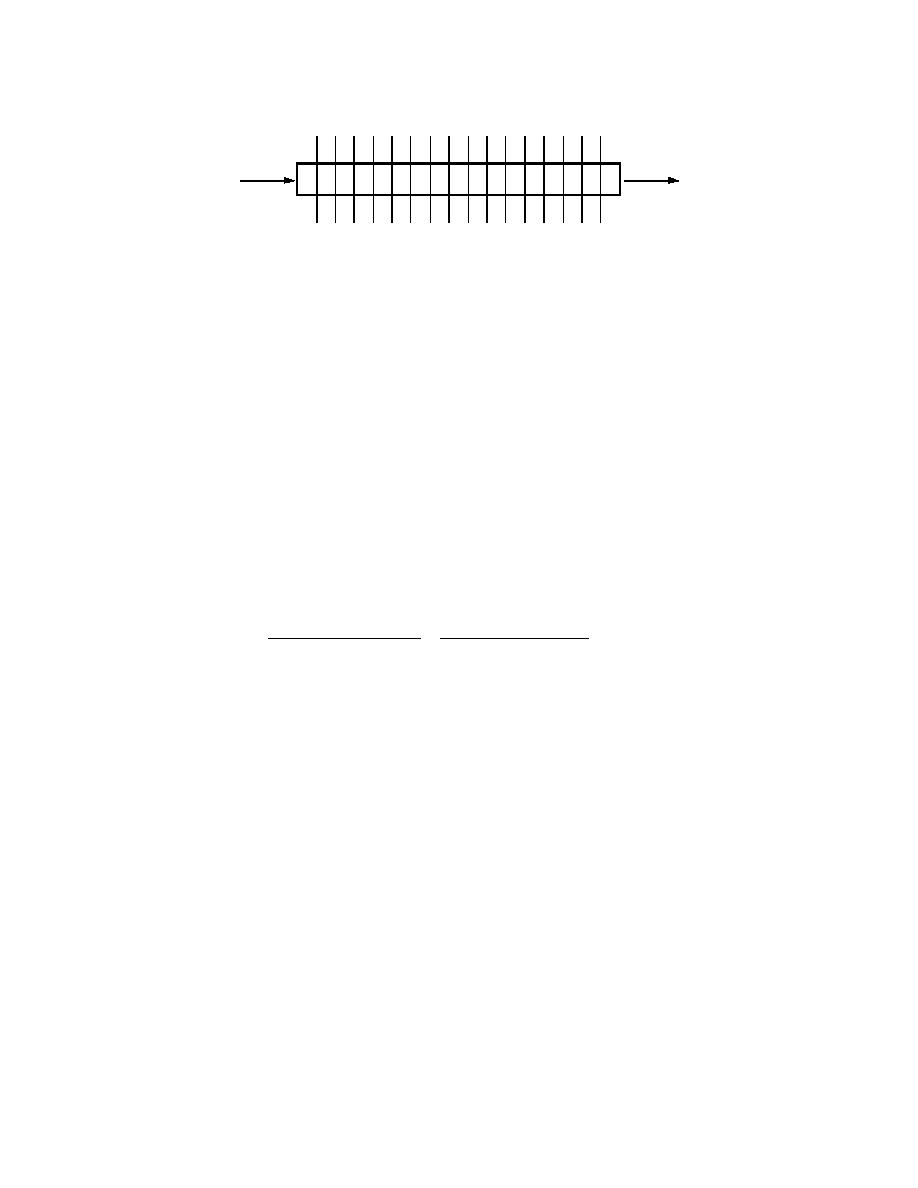
Air Temperature
Return
Supply
Temperature
Temperature
Figure 3. Schematic of a hydronic heating system radiator.
q2/q0 = [(Tml)1/(Tml)0]n1 [(Tml)2/ (Tml)1]n2
(3-1)
where q = heat output from the radiator (W)
Tml = logarithmic mean temperature difference (C)
n1, n2 = empirically determined coefficients (dimensionless).
and the subscripts denote the following operating conditions
0 = "design" condition for the radiators, usually the maximum load condition
at maximum supply temperature
1 = condition of actual supply temperature with the flow rate as determined
under the design condition
2 = any actual operating condition.
Equation 3-1 uses the logarithmic mean temperature difference Tml and exper-
imentally determined constants to predict heat exchanger performance. The log-
arithmic mean temperature difference is defined as
(Ts - Ta ) - (Tr - Ta ) =
Ts - Tr
Tm1 =
.
(3-2)
l n(Ts - Ta ) - ln(Tr - Ta ) l n[ (Ts - Ta )/(Tr - Ta ) ]
One problem that results from using the logarithmic mean temperature differ-
temperature. This limits the extent of closed form analysis and ultimately, when
calculations are required, it forces solution by iterative numerical methods. As a
solution to these problems, the use of the arithmetic mean as an approximation for
the logarithmic mean was proposed by Soumerai (1987). The arithmetic mean
temperature difference for this case is defined as
Tma= [(Ts Ta) + (Tr Ta)]/2 = (Ts + Tr 2Ta)/2.
(3-3)
The arithmetic mean temperature difference has the advantage that it can be used
return temperature Tr given the value of the arithmetic mean temperature differ-
ence. The disadvantage of using the arithmetic mean temperature difference as an
approximation for the logarithmic mean temperature difference is the error induced
by this approximation. As Soumerai (1987) points out, within certain ranges of the
temperatures involved, the resultant errors are usually acceptable, given the other
uncertainties in heat transfer engineering. Soumerai (1987) recommends the use of
the arithmetic mean as an approximation for the logarithmic mean in cases where
the approach factor AF is equal to or greater than 0.5. The approach factor for this
type of heat exchanger is given by
18



 Previous Page
Previous Page
