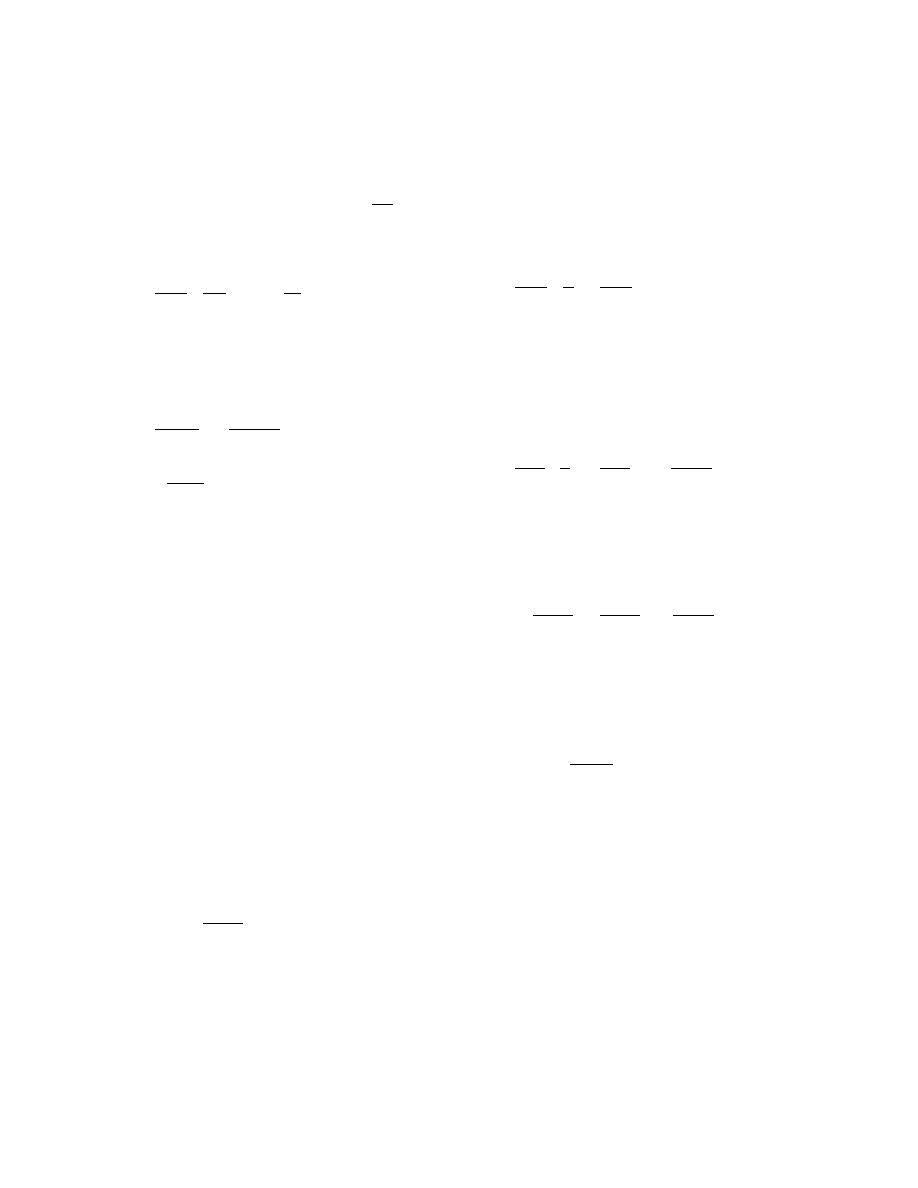
To make solving eq 22 easier, R92 assumed that
Displacement height
c1 = c2 = c; for c he used 0.25, which provided the
To convert the total drag coefficient CDh to its
best fit to the data that he tested his model
10-m value, we need to know the wind speed
against. With this assumption, eq 22 reduces to
profile law. When a surface is covered with
roughness elements that are much larger than z0,
[C
]
^ (Φ) exp-cλ(Φ) Uh . (23)
τ(Φ) =
ρUh
+ λ(Φ)CR
2
it is often necessary to include a displacement
Sh
u*
height d (Thom 1971) in the semi-logarithmic
Notice
wind profile. That is
U(z) 1 z - d
u2
τ(Φ)
= ln
1
(29)
= * ≡ CDh ≡ 2
(24)
k z0
u
ρUh Uh
2
2
r
*
where U(z) is the average wind speed at height z.
is the drag coefficient for the total surface stress
But near the tops of the roughness elements,
referenced to height h. On inserting this defini-
eq 29 cannot be accurate because of the enhanced
tion and rearranging terms in eq 23, we get
turbulence there created by flow around these
obstacles. R92 therefore hypothesized that, for
cλ(Φ)r
-cλ(Φ)r
h ≤ z ≤ zw
exp
2
2
U(z) 1 z - d
z - d
+ ψ
= ln
cλ(Φ)
(30)
[
]
-1/ 2
zw - d
CSh + λ(Φ)CR (Φ)
k z0
^
=
u
(25)
.
*
2
where ψ is a profile influence function similar to
This has the form
the stability corrections required by Monin-
Obukhov similarity. At zw and above, ψ is zero.
X eX = a
(26)
R92 went on to show that
where a is a constant for a given value of Φ.
z-d
z -d
z - zw
I solved eq 26 for X using Newton's method;
(31)
ψ
+ ln w
=
z-d
zw - d
zw - d
the solution required only two to three iterations.
There are multiple solutions to eq 26, however;
and that
we must select the right one. As R92 explained,
eq 26 has the following properties:
zw d = cw(h d)
(32)
For 0 < a < e1, eq 26 has two solutions, X1 and
X2, where X1 < 1 and X2 > 1.
where cw is a constant. He also defined
For a = e1, X = 1.
For a > e1, there is no solution to eq 26.
h-d
= ln(cw ) + cw - 1
ψ h ≡ ψ
1
(33)
The only nontrivial case is the first of these; and
zw - d
X1 is the only physical solution, since X must ap-
proach zero as either λ(Φ) or a approaches zero.
which will be useful shortly. Notice, there are er-
Thus, to start Newton's method, my first guess
rors in two of R92's equations (eq 29 and 31). In
was X = a.
an unpublished correction to his paper dated 23
Solving eq 26 yields X, which, in turn, is relat-
October 1992, Raupach explained that, in light of
ed to the total drag coefficient we seek
these errors, cw is approximately 4 rather than
1.5, the value he originally gave. Hence,
ψh = 0.64, a value independent of surface proper-
2X
CD1h 2 =
/
.
(27)
cλ(Φ)
ties.
Equation 32 implies that
Notice, to check this solution, we can make an
zw = cw h + (1 - cw )d.
asymptotic approximation in eq 23. When λ(Φ) is
(34)
near zero
With cw = 4 and the assumption that zw > h, eq 34
implies that d < h: The displacement height is al-
CDh = CSh + λ(Φ)CR (Φ).
^
(28)
ways less than the height of the roughness ele-
ments.
6



 Previous Page
Previous Page
