Figure 4. Log-transformed TNT concentrations from sampling location 1-linear model with intercept

Table 1. Continued - SR96_150016

Table 2. Results from sampling location 2, Monite site

SR96_15
Page Navigation
11

r = 0.999

Slope = 0.926

y-intercept = 0.251

Laboratory Results (log g/g)

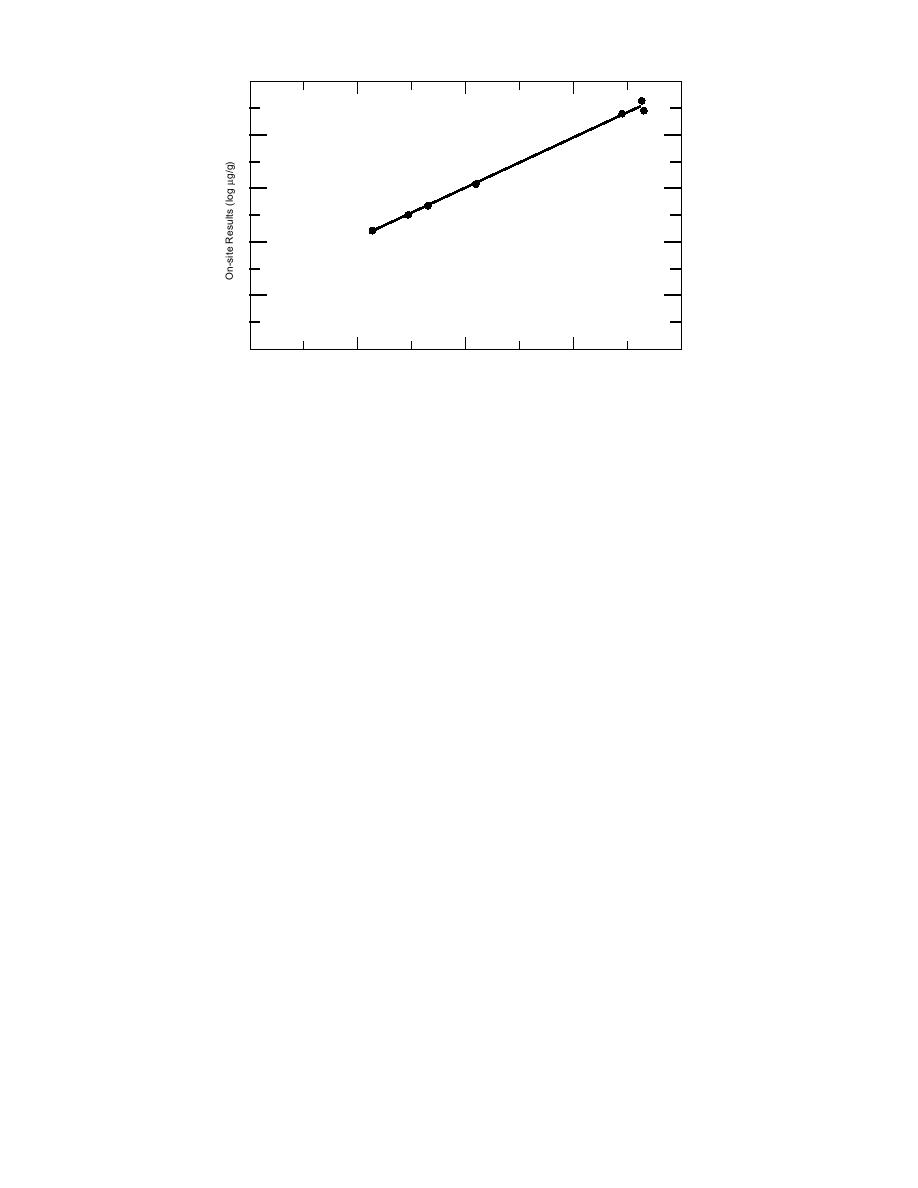
Figure 4. Log-transformed TNT concentrations from sampling location 1--

linear model with intercept.

one another, except samples 1 and 4. Thus, for

intercept, and for the log-transformed values with

sampling location 1, very similar conclusions were

intercept (Table 1b). Correlation coefficients were

reached regarding the nature of the analyte distri-

0.973, 0.973 and 0.999 for untransformed data with

bution using either the results of on-site analyses

and without intercept and the log-transformed

or results of laboratory analyses.

data respectively. The correlation coefficient for

Because the mean concentrations and absolute

the zero intercept model is identical to that for the

analytical variances for various samples from site

model with non-zero intercept, and we interpret

1 differ so drastically, it is not possible to directly

this to mean that the intercept is not significantly

compare the uncertainties introduced by sam-

different from zero and that the accuracy of the

pling with those from analysis by partitioning

field method vs. the lab method can be estimated

variances of untransformed data using normal

from the slope of the best fit linear least squares

distribution statistics. ANOVA of the log-trans-

line (81.5%). The excellent correlation for the log-

formed data indicates that even the log concen-

transformed data, as shown in Figure 4, demon-

trations from various samples differ significantly

strates the equivalency of the results for the two

from one another, using analytical error as the

methods over several orders of magnitude of con-

yardstick.

centration.

A simple way to compare sampling and ana-

Paired t-tests were also conducted on the seven

lytical uncertainties is to compare the ratios of

mean values and the log-transformed mean data

extreme mean concentrations obtained for the

for the two methods of analysis (Table 1b). The t-

seven samples with those for duplicate analyses

value for the untransformed data was 1.35 and

from the same location. For location 1, the ratio of

that for the log-transformed data was 0.07, nei-

highest mean concentration to lowest mean con-

ther significant at the 95% confidence level. We

centration was 243 for the field analyses and 304

must acknowledge that comparison of the

for the laboratory analyses. The highest ratios for

untransformed results is not truly legitimate be-

duplicates were 1.16 for the field analyses and

cause the concentration distribution is non-

1.47 for the laboratory analyses. Thus, for this

Gaussian. Results of the paired t-tests agree with

location, sampling error contributes many times

those from correlation analysis, i.e., the labora-

more uncertainty than analytical error for either

tory and on-site results compare very favorably.

field or laboratory analysis.

Results of the analyses of the composite samples

Results for the field and laboratory analyses of

at sampling location 1 were also quite interesting.

these discrete samples were compared in two

The mean and standard deviation of the seven

ways. Linear correlation analysis was conducted

on-site analyses for the composite was 13,100

532 g/g in comparison to the mean of the

using the untransformed data with and without

Index

Privacy Statement
Press Release
Contact