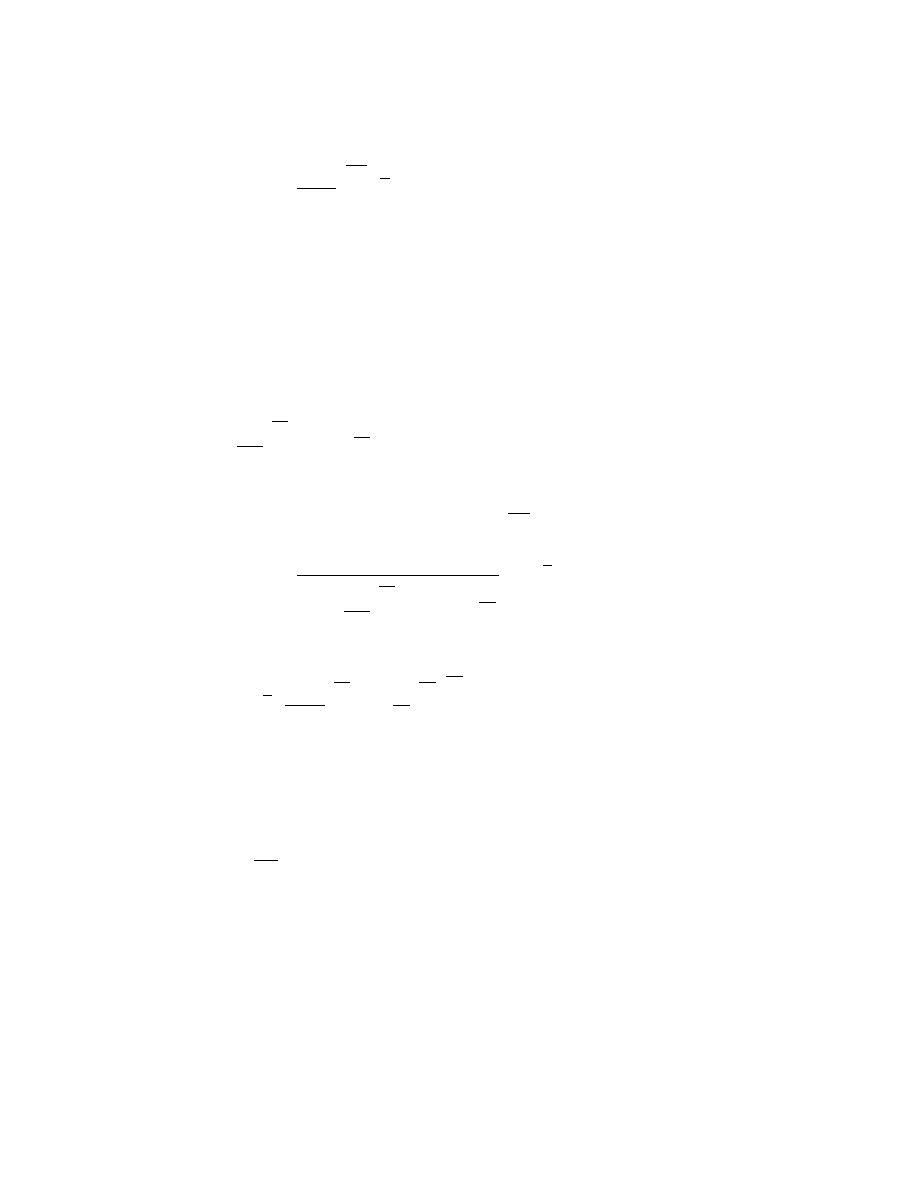
Therefore, as found before, (derived with constant volume, but still applicable with a time
varying volume),
1-nc
⎛ nc -1 ⎞
nc
xA2 (τ 2 ) = κ cf ⎜
1
⎟ τ2
(7.31)
nc
A2 ⎠
⎝
where now A2 is a function of time. Therefore, define a constant AII equal to the initial
mobile water volume of the U2 wave, and a new variable ∆2 equal to the total water
volume the U2 wave has absorbed, by the equation
A2 = AII + ∆2
(7.32)
where we know that because the U1 wave is undisturbed beneath the U1 U2 junction, the
total water volume below the junction must be the same as it would be were the U2 wave
not present, giving rise to the conclusion that the total water volume above the U1U2
junction must be equal to the initial volume of the U2 wave plus the volume of the U1
wave, which would not otherwise have passed the U1U2 junction point. This means that
nc
⎡x ⎤
nc-1
∆2 = ⎢ A2 ⎥ ( nc - 1)τ11-nc .
1
(7.33)
⎢ κ cf ⎥
⎣
⎦
By substituting into Equation (7.32) we get
1-nc
⎛
⎞
nc
⎜
⎟
⎜
⎟
nc - 1
xA2 (τ 2 ) = κ cf ⎜
1
τ2 ,
⎟
(7.34)
nc
nc
⎜
⎟
⎡x ⎤
nc-1
⎜ AII + ⎢ A2 ⎥ ( nc - 1) (τ1 )1-nc
1
⎟
⎜
⎟
⎢ κ cf ⎥
⎣
⎦
⎝
⎠
which can be solved for xA2
1-nc
nc-1
⎡ ⎛τ ⎞ ⎤
1
nc
⎛ A ⎞
nc-1
nc
1
⎢1 - ⎜ 2 ⎟ ⎥ .
= κ cf τ 2 ⎜ II ⎟
(7.35)
xA2
nc
⎢ ⎝ τ1 ⎠ ⎥
⎝ nc - 1 ⎠
⎣
⎦
This is the form used in the model to find the depth of any wave that has a preceding
wave. Finding the point at which one wave of volume flux completely overtakes its
antecedent proves to be straightforward if the first wave has no predecessor, with the
result being
-1
⎡⎛ A
⎤
nc -1
⎞
τ 2 = δ ⎢⎜
+ 1⎟ - 1⎥
(7.36)
II
AI
⎢⎝
⎥
⎠
⎣
⎦
where δ is the time between the formation of wave U1 and wave U2. This gives us the
ability to calculate the flux as a function of depth and time resulting from a single water
volume input, to calculate the depth and net water volume of a following input wave of
volume flux, and to calculate the depth and time at which one wave of volume flux will
overrun a preceding wave of volume flux. In short, it is now possible to completely
describe the saturation and flux resulting from two point inputs in several compact
equations, without any finite difference or finite element matrix solutions to differential
equations. In order to extend the model to the general case in which many waves may be
62



 Previous Page
Previous Page
