Governing Equations of Flow within the Snow-continue - SR04-10080

Governing Equations of Flow within the Snow-continue - SR04-10079

Governing Equations of Flow within the Snow-continue - SR04-10081

SR04-1
Page Navigation
61

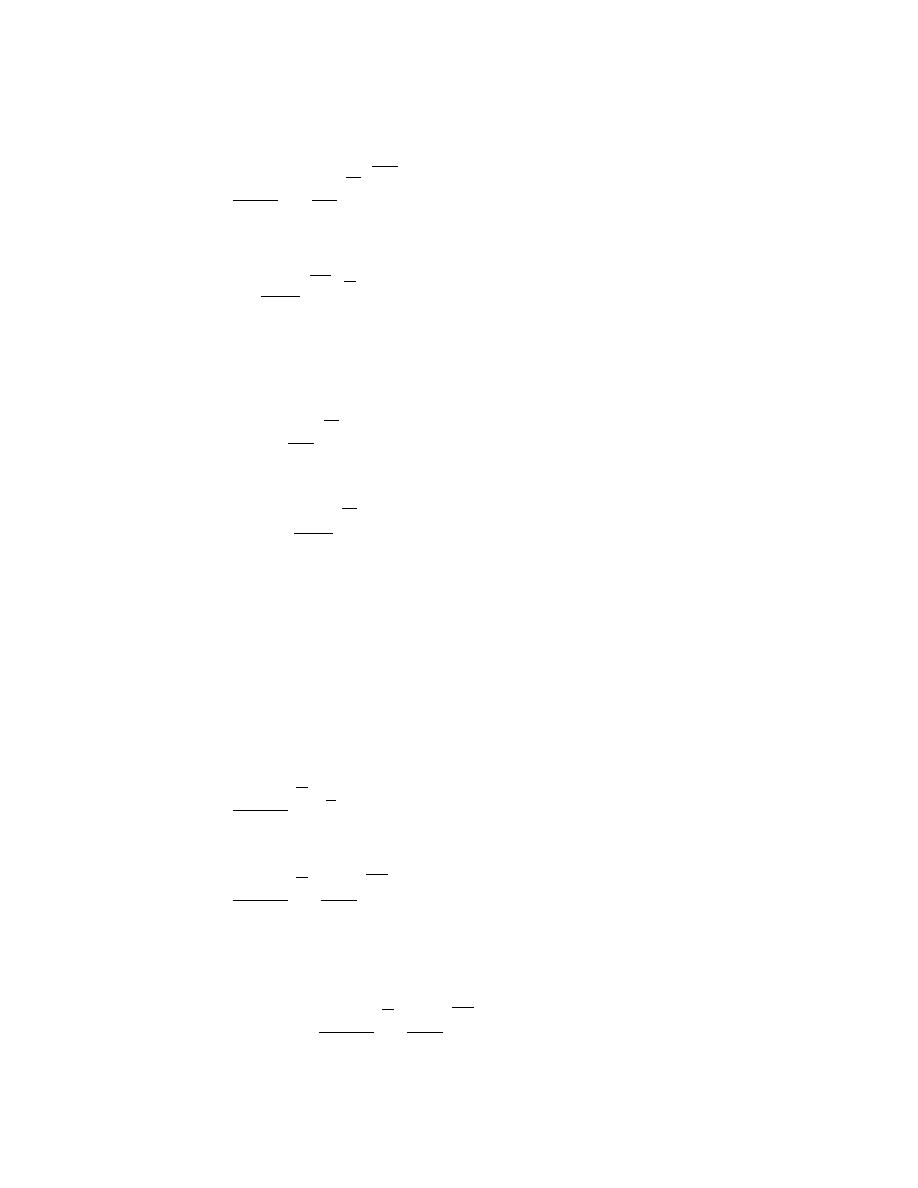
The solution to this integral gives the time required for a wave of volume flux to

penetrate to depth D

κ cf ⎞ηcf ⎟

For modeling purposes, note that Equation (7.21) may also be written in the simpler form

xU = κ cf ⎜ c ⎟ τ nc .

Having depth of penetration as a function of time, and vice versa, requires only that the

effects of preceding flux waves be incorporated in order to construct a working model of

water movement through homogeneous snow. Therefore, consider two flux waves, each

proceeding according to Equation (7.18)

U1 ( χ1 ,τ1 ) = ⎜ 1 ⎟

U 2 ( χ2 ,τ 2 ) = ⎜

Assume that χ1 - χ2 = ε > 0 (that the wave U1 began at an earlier point in time than the

wave U2). Since there is no singularity within the region over which the U2 solution

applies, flux will be continuous and differentiable over this region, up to the singularity

caused by the U1 U2 junction. As the U2 wave flows through the snow, Equation (7.25)

must always be met, even as new water volume is absorbed into wave U2 from the

residual saturation of wave U1. Therefore, to accommodate the new water volume the

second wave has encountered while still maintaining its solution to the conservation and

flux-saturation equations, the volume flux wave U2 must travel deeper into the snowpack

than it otherwise would, thereby encountering more residual saturation in the process.

Numerically, the residual saturation encountered will take the form

⎣ ρwkw0 g ⎦

which, when combined with U1 from Equation (7.26), becomes

⎡ ηw ⎤ ⎛ χ1 ⎞

ρwkw0 g ⎥ ⎜ κ cf τ1 ⎟

which means that if xA2 is the deepest point within the snow at which the U2 solution

applies, (the point of the singularity), then the volume of water absorbed by the U2 wave

in moving some infinitesimal distance through the snow will be given by

∂ A2 = φ (1 - Swi ) ⎢

Western Governors University

Privacy Statement
Press Release
Contact

Integrated Publishing, Inc. - A (SDVOSB) Service Disabled Veteran Owned Small Business