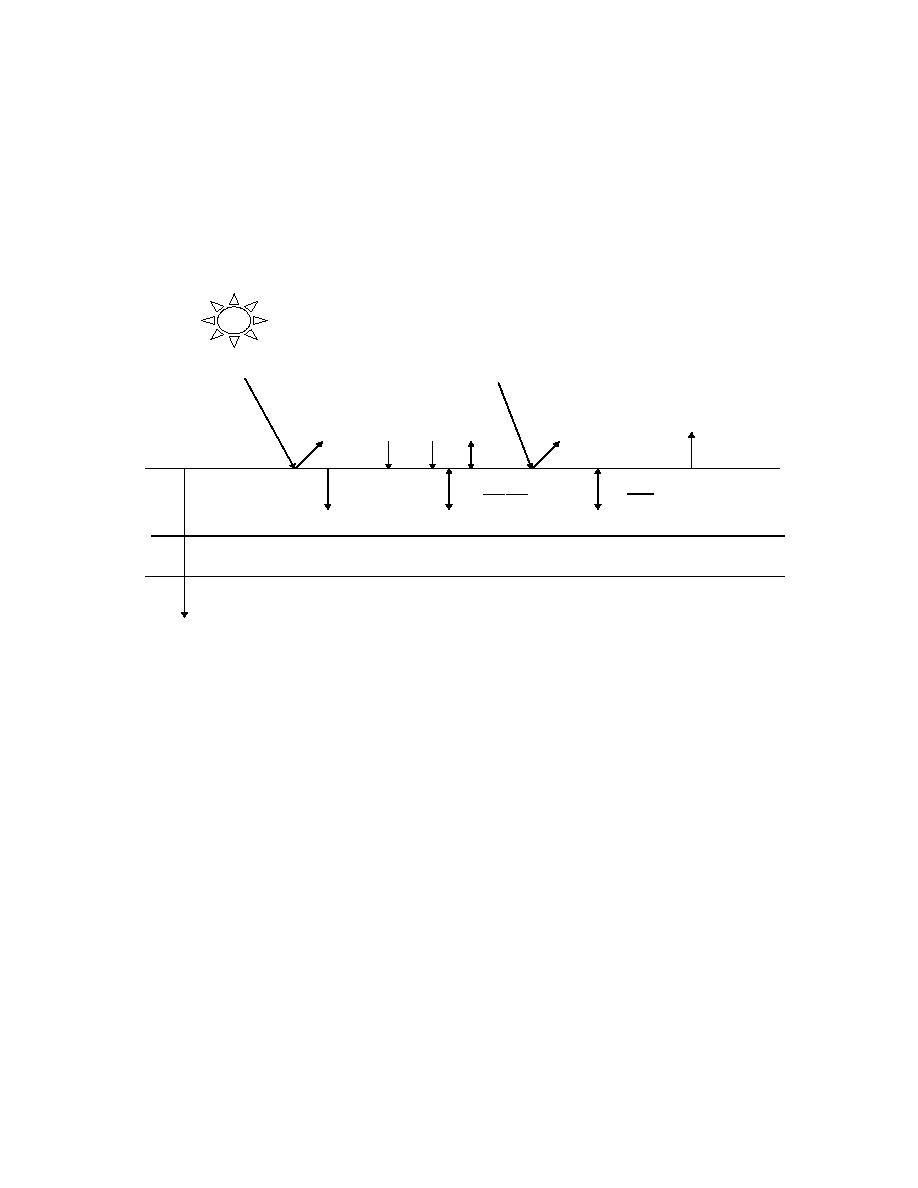
the presence of wind. The precipitation heat represents the energy needed to cool or heat
any snow or rain that falls on the surface. The first term in the second row of Equation
(4.2) takes care of heat conduction to/from the surface by the underlying ground
depending on the temperature gradient. This is followed by the heat released/absorbed by
the soil as the soil moisture melts/freezes. Finally, the last term represents heat that is
advected away from/towards the surface as a result of the vertical movement of moisture.
Is ↓
I i↓
r
(1- ε )Ii↓
α Is ↓
εσ T 4
L
P
H
r
z=0
∂T
ρ ∂θ
κ
i
i ∆z
vcpT
l
fu s ρ w ∂ t
∂z
L ayer 1
L ayer 2
L ayer 3
Figure 4.1 Surface Energy Balance.
4.1.1 Solar Radiation
I s ↓= I s ↓dir + I s ↓dif . Since most surfaces are not horizontal, the effect of slope on the
amount of solar radiation that impacts a site must be taken into consideration. The
position of the sun is determined by the solar zenith angle, φo, and the solar azimuth
angle, ϑ0 as measured clockwise from North to its horizontal projection. Similarly, the
slope is defined by φ, the zenith (elevation) angle of the surface as measured in the
positive direction upwards from the horizontal and ϑ , the azimuth or aspect angle
measured positive clockwise from North to its horizontal projection. Refer to Figure 4.2
for clarification. Following the work of Jordan (1991) and Shapiro (1978) the following
29



 Previous Page
Previous Page
