Assuming that η = 1, we will calculate several important parameters of Kanto loam as
s3 = 4.25 cm ⋅ d ⋅ C/g, σc = 453 kPa,
σx = 998 kPa.
(219)
We anticipate that water expulsion occurs if σ > 453 kPa. In order to calculate h and hw by eq
160 and 161, respectively, we must determine T1. Using eq 212, 213 and 214, we will reduce
eq 98 to
F{y(T1), α o ,Vo , σ, δo } = 0.
(220)
A detailed description of F is given elsewhere (Nakano and Primicerio 1995). Since eq 220 is
a nonlinear algebraic equation, for given αo , δo, σ and Vo, T1 was calculated numerically by
the Newton-Raphson method.
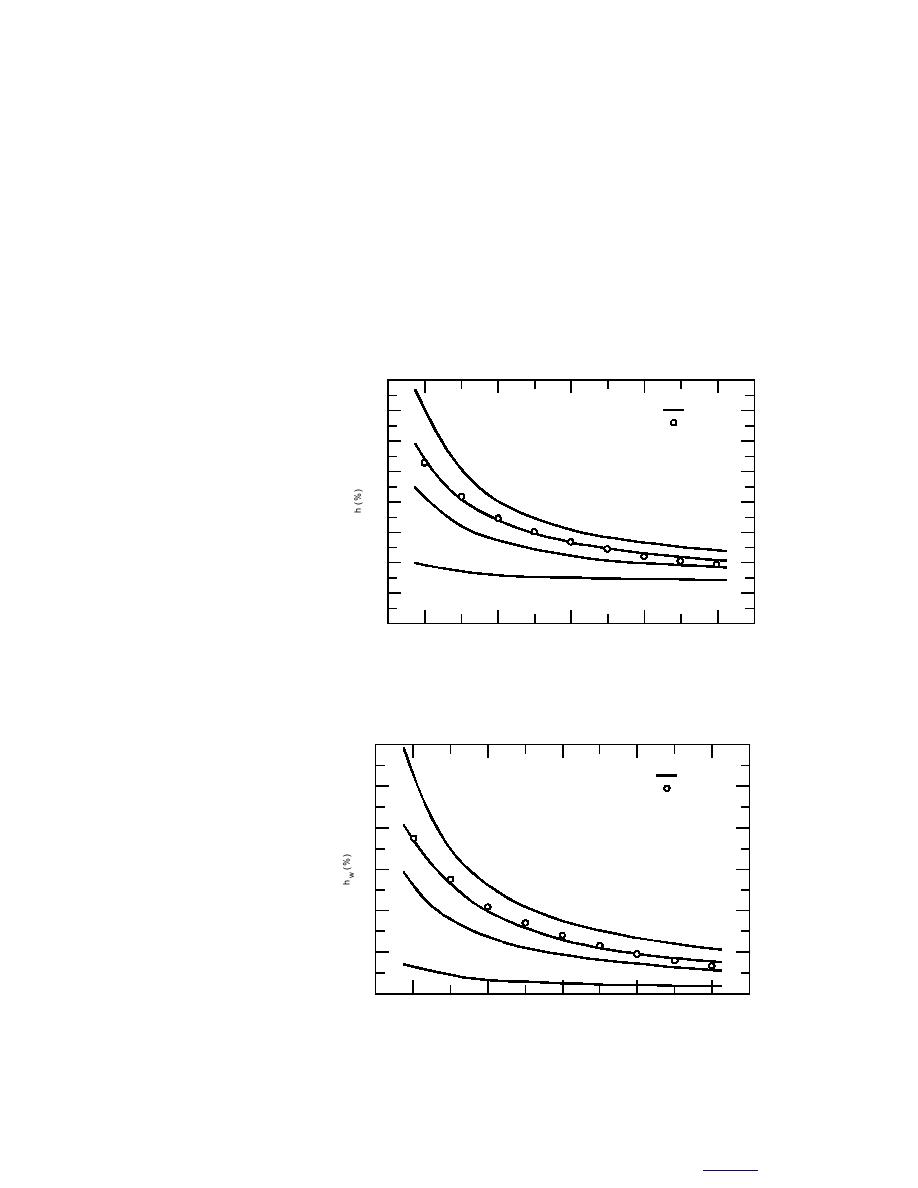
Calculating h and hw as
18
functions of Vo for various
σ = 500 kPa
αo = 1.0 (C . cm1)
sets of (αo, δo, σ) with the
Predicted
16
Empirical
ranges of 0.1 ≤ αo ≤ 1.0C/
14
cm, 0.5 ≤ δo ≤ 5.0 cm, and 0
≤ σ ≤ 1.5 MPa, we have
12
found that the dependence
of h and hw on σ is the
10
0.75
strongest, and then less
8
0.50
strong on Vo, αo and δo in
6
0.10
order of decreasing depen-
dence. The value of δo is
4
proportional to the resis-
tance against the flow of
2
2
4
6
8
10
water in Ro. On the other
. d1)
Vo (cm
hand, the flow resistance Figure 4. Calculated values of h (%) vs. V (cm/d) under four dif-
o
of R1 increases with in- ferent values of α with δ = 1.0 cm and σ = 500 kPa. Circles are
o
o
creasing σ. When the resis- calculated by an empirical formula (Ryokai 1985).
tance of R1 becomes much
greater than that of Ro, the
12
effect of δo diminishes. The
σ = 500 kPa
αo = 1.0 (C . cm1)
effect of δo was found neg-
Predicted
10
Empirical
ligible when σ is greater
than 300 kPa. The calculat-
8
ed values of h vs. Vo and
hw vs. Vo for Kanto loam
6
under the condition of σ =
500 kPa, and δo = 1.0 cm
0.75
4
with four different values
of αo are presented in Fig-
0.50
2
ure 4 and 5, where circles
0.10
are values calculated by
the empirical formulas for
0
2
4
6
8
10
Kanto loam determined by
1
Vo (cm . d )
Ryokai (1985). From Fig- Figure 5. Calculated values of h (%) vs. V (cm/d) under four
w
o
ure 4 and 5 we find that the different values of αo with δo = 1.0 cm and σ = 500 kPa. Circles are
effect of αo on h and hw is calculated by an empirical formula (Ryokai 1985).
29
Contents




 Previous Page
Previous Page
