The empirically determined values of parameters in eq 212, 213, and 214 for Kanto loam
(Nakano and Takeda 1994) are wo = 0.740, A = 1.5 10 4 C, b3 = 0.110, Ko = 1.77 103 g/
(cm⋅d⋅MPa), b1 = 0.520, K20 = 1.98 103 g/(cm⋅d⋅C) and b2 = 1.04.
The existence of the boundary Cs (Fig. 2a) has been verified empirically for three types
of soils including Kanto loam under σ = 0 (Takeda and Nakano 1990). According to Prop. 2,
Ts is a decreasing function of σ. This implies that the region Si decreases as σ increases,
which is also verified by the data of Kanto loam (Takeda and Nakano 1993). We will con-
sider a freezing test in which a soil sample with a uniform initial temperature Ta > 0C is
frozen from the bottom up while the bottom temperature is kept constant at Tb < 0C and
the top temperature at Ta. The temperature field changes rapidly at the start of the test.
However, as time elapses, the rate of the change slows down so that the transient freezing
may be approximated by a series of quasi-steady freezing steps. Hence, the later part of the
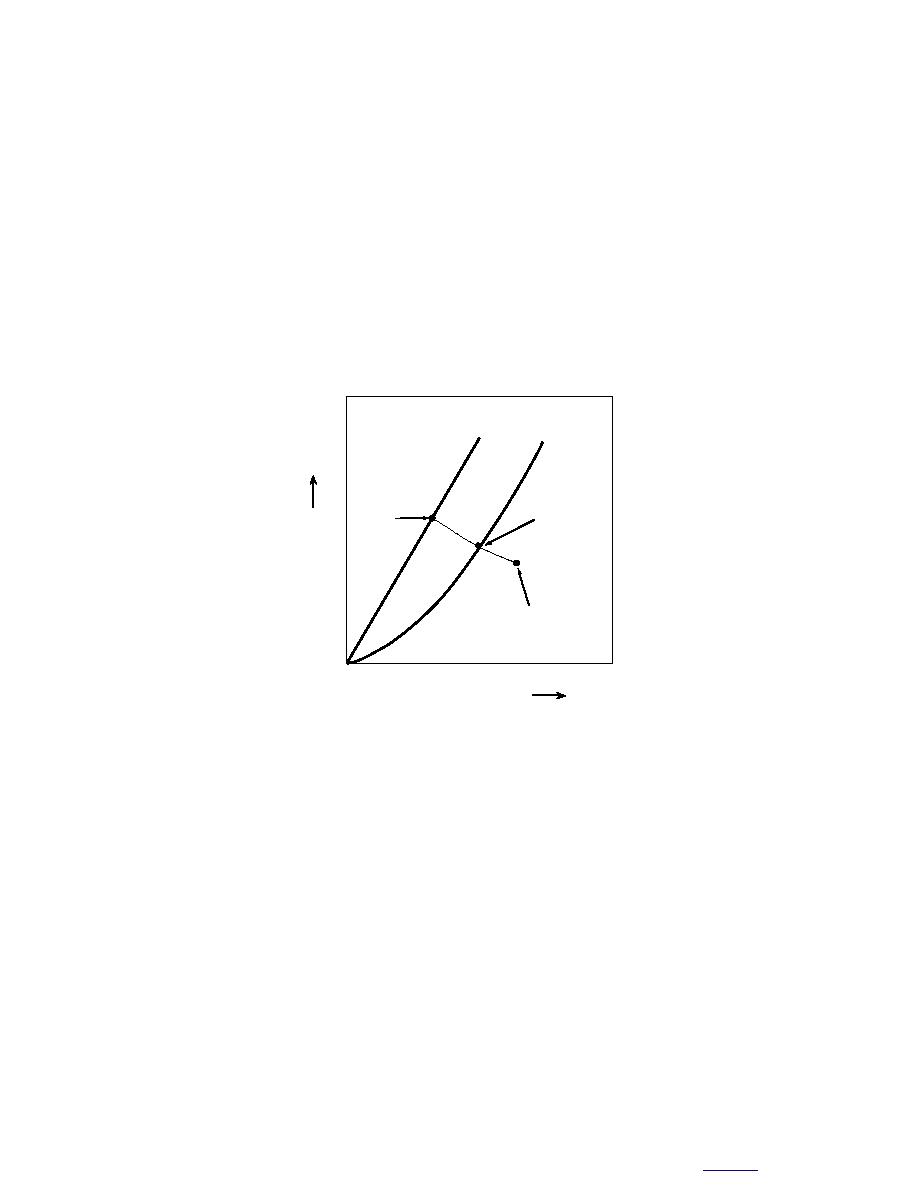
experiment can be represented by a trajectory in Figure 3, consisting of points
α(t) = {α1(t), α o (t)} for t2 ≥ t ≥ to .
Le
Cs
Si
Sp
α(t2)
α(t1)
αo
α(t)
α(to)
0
α1
Figure 3. Trajectory of α(t).
A point α (to) is in Sp where frozen soil without any visible ice layer grows. As α1
decreases and αo increases with time, the trajectory approaches the vicinity of α(t1) in Sp.
The pattern of ice-rich frozen soil grown in this vicinity evidently depends on the soil type
loam, for instance, clearly indicate that the pattern of rhythmic ice banding is formed at the
small values of α1, while soil particles or small aggregates of soil particles are evenly dis-
persed at the greater values of α1. The mechanism of such pattern formation is not well
understood, but possible causes include the heterogeneity of soils and instabilities in the
coupled heat and mass transport process with phase change. The quasi-steady solution
described above predicts the average ice content of frozen soil and accounts for the growth
of an ice layer but not the time-dependent formation of patterns.
When α(t) reaches α(t1) on Cs, an ice layer emerges. While α(t) moves toward α(t2) on Le,
the growth of the ice layer continues with decreasing growth rate until α(t) reaches α(t2) on
Le where the ice layer stops growing. At α(t2) fo vanishes and we find from eq 59 and 60 that
eq 76 is reduced to
σ = -γ Tσ .
(215)
27
Contents




 Previous Page
Previous Page
