set βm = βh. The bulk coefficient ratios corresponding to eq 42a,b,c can be derived and expressed as
-2
3 / 2
ch cm
= 1 + βm
Rib
cm
,
c
ch,n m,n
cm,n
-1
-3 / 2
1/ 2
cm
c
ch
1 + βh ch
Rib , and
= m
(43a,b,c)
ch,n cm,n
ch,n cm,n
-1
-3 / 2
1/ 2
c cm
c
ch
1 + βh h
Rib .
= m
ch,n cm,n
ch,n cm,n
Using eq 43a,b, a relation involving cm/cm,n with βm, βh, and Rib can be derived as
1/ 2
βm cm
β2
βm cm
+ 1 - m Rib = 0 .
1 -
-2
1 -
(44)
2βh cm,n
βh cm,n
βh
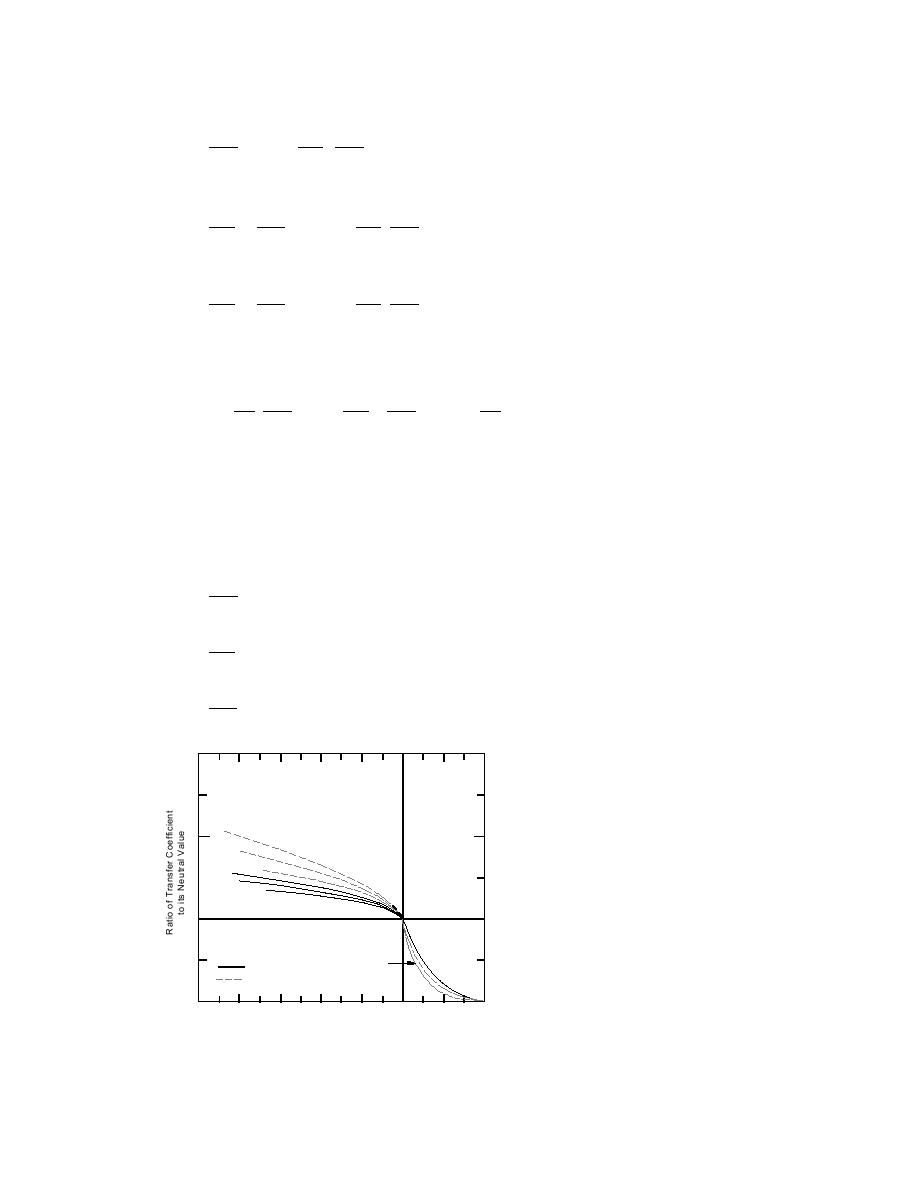
Figure 2 shows the ratio of the transfer coefficient to its neutral value over a wide range of Rib. It
can be seen that, unlike the unstable case, the curves for the stable case calculated based on βm = 7,
βh = 11, and βw = 20 are independent of cm,n. The sudden change of slope around Rib = 0 is due to
the fact that the values of βm and βh are not equal to γ/4 and γ/2, respectively (γ = 16).
Deardorff (1968), for practical purposes, approximated the bulk transfer coefficient (over water)
for the stable case by
(
)
cm
= exp -2βm Rib ,
cm,n
[
]
ch
= exp - (βm + βh ) Rib , and
(45a,b,c)
ch,n
[
]
cw
= exp - (βm + βw ) Rib ,
cw,n
3
c m,n = 0.0016
2
0.0012
0.0008
0.0016
0.0012
0.0008
1
Figure 2. Ratio of bulk transfer coeffi-
cient to its neutral value from diabatic
profile theory, over a wide range of bulk
cw / c w,n
cm / cm,n
ch/ ch,n
Richardson numbers. cw / cw,n is not shown
on the unstable side for the fact that it will
0
0.5
0.4
0.3
0.2
0.1
0
0.1
0.2
coincide with ch / ch,n if Kw = Kh and with
(unstable)
(stable)
cm / cm,n if Kw = Km (after Deardorff 1968).
Ri b
10



 Previous Page
Previous Page
