x
Air
Ta , U,
b
φ
y
L
Condensate
Film
w
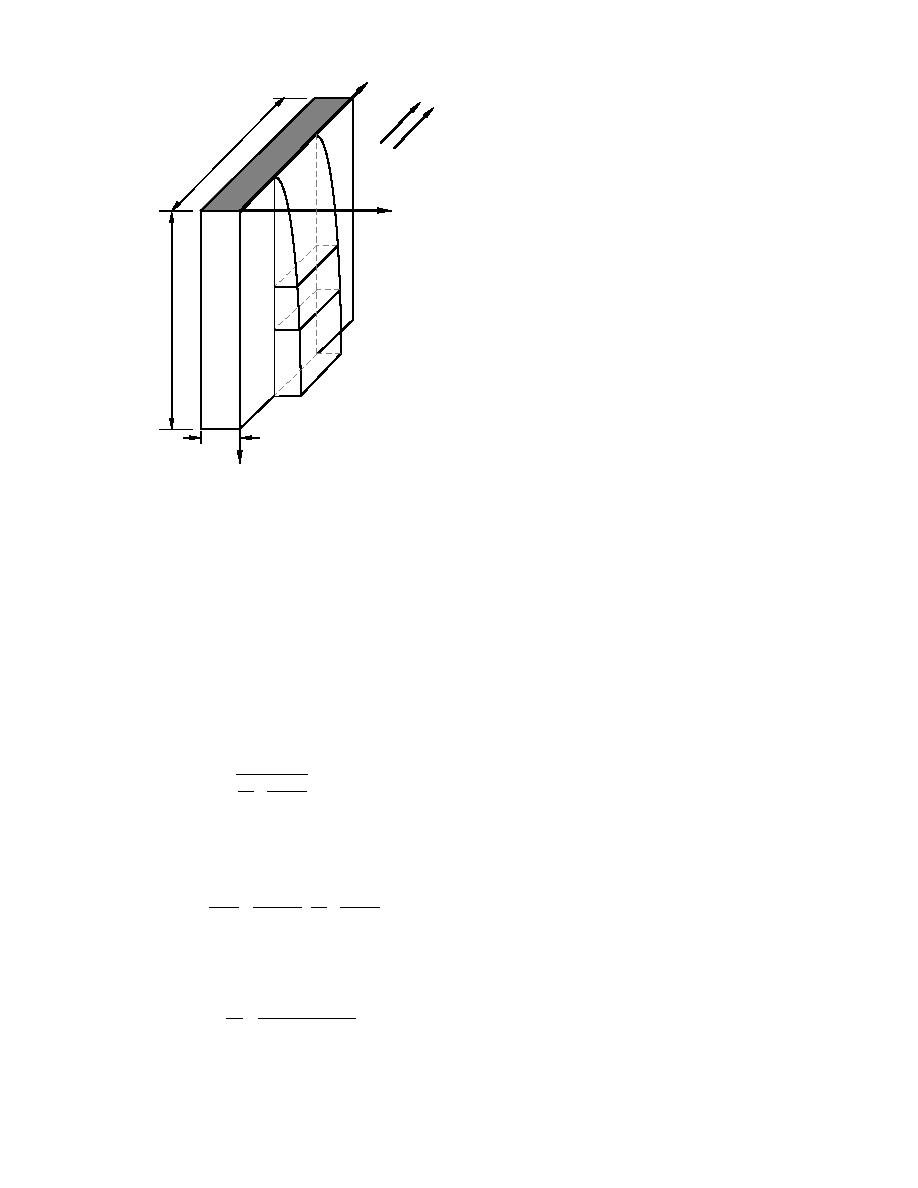
Figure 13. Dehumidification of air on a vertical
z
rectangular fin.
taken into account by multiplying the single-phase heat transfer coefficient h by an inter-
determined experimentally. Since the minimum value of Cf is unity (for smooth interface
at low vapor velocity), the use of Cf = 1 would be conservative. The effect of mass transfer
on the temperature profile is taken into account by introducing the Ackermann correction
factor Ca. Thus, the sensible heat flux, qs′ , between air and condensate film can be ex-
′
pressed as
qs′ = CfCah(TaTi) .
′
(67)
′ ′
for qt′ becomes
′
(Ta - Tf ) .
qt′ =
(68)
′
δ
R
+
kl CfCah
Substituting for qt′ from eq 68 into eq 65, the differential equation governing the tem-
′
perature distribution in the fin becomes
-1
d2Tf 2(b + w) δ
R
(Ta - Tf ) = 0 .
+
k + C C h
(69)
kwb l
fa
dz2
The momentum eq 14 for the condensate film can be adapted for the present analysis as
follows:
l (1 - R) qt′
dδ
′
=
δ2
.
(70)
dz gρl (ρl - ρv ) hfg
21



 Previous Page
Previous Page
