1.0
Dry
Surface
0.8
80% RH
0.6
η
90
99
0.4
0.2
Figure 12. Efficiencies of dry and wet
radial fins. Adapted from Elmahdy
0
0.2
0.4
0.6
0.8
1.0
and Biggs (1983).
N
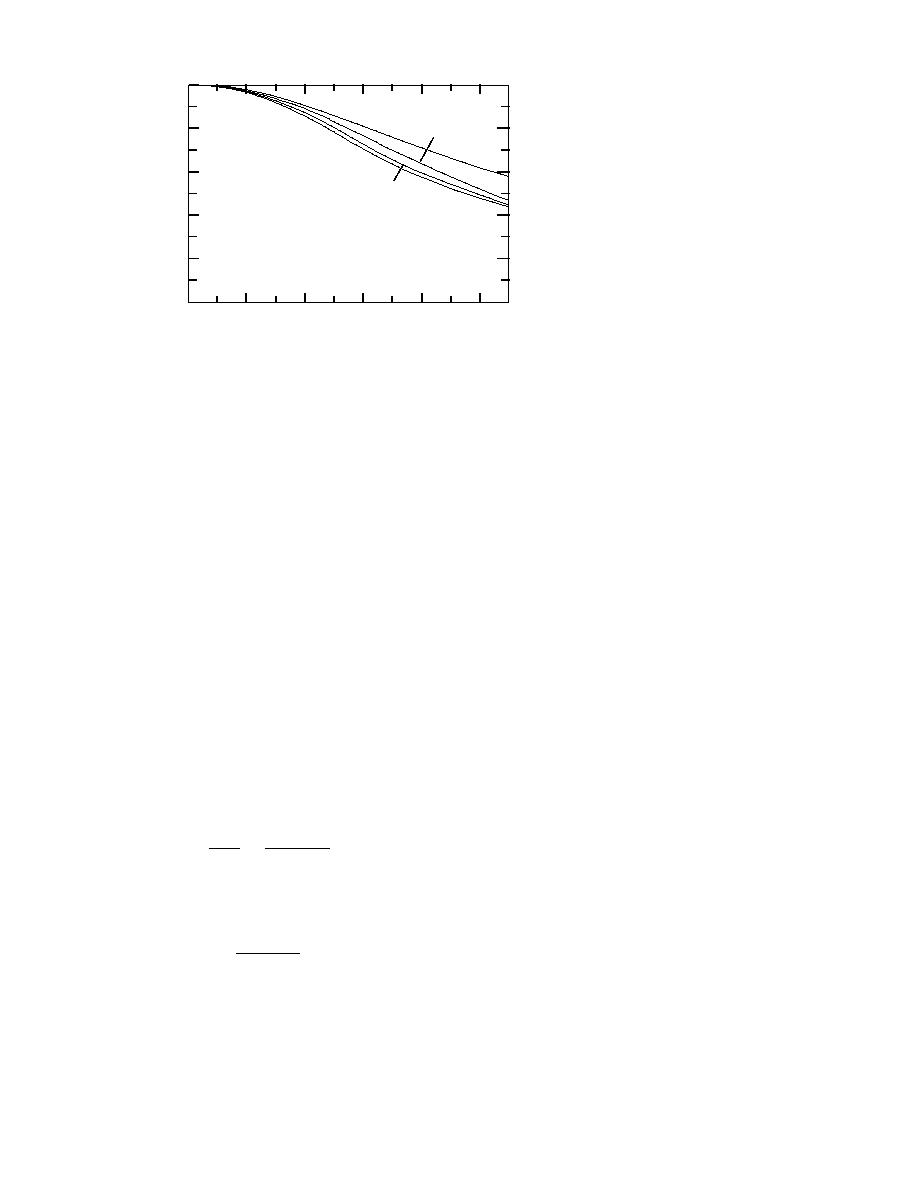
The ratio of q/qideal gives the efficiency of the fin. Figure 12 shows the efficiency as a
function of N for both dry and wet fins. This figure is based on the same data as used in
Figure 11. The efficiency of a wet fin can be seen as lower than that of a dry fin, and
decreases as the relative humidity increases. This can be explained as follows. As the
relative humidity increases, the driving potential for mass transfer increases that, in turn,
causes qideal to increase. The corresponding actual q, however, does not increase by the
same amount. The net result is a decrease in η.
Conjugate models
This section describes two conjugate models for a cooling and dehumidifying vertical
fin of rectangular profile. The first model from Coney et al. (1989a) allows for the coupling
between the fin temperature and the condensate film, but assumes the convective heat
transfer coefficient to be constant. The approach is essentially the same as in Simple
Models, except that the model of Coney et al. also includes the effect of mass transfer in
writing the energy balance for the fin. The second model described by Kazeminejad et al.
(1993) neglects the thermal resistance of the condensate film but allows for the heat
transfer coefficient h to vary along the fin. The model finds the variation of h through the
solution of boundary layer equations. Both models are discussed in sections that follow.
Coney et al. model
The model considers a vertical rectangular fin as depicted in Figure 13. Taking a slice of
fin of volume bwdz and equating the net energy conducted through the slice to the energy
convected to the surface 2(b + w)dz by simultaneous heat and mass transfer, gives
2 (b + w) qt′
d2Tf
′
=-
(65)
2
kwb
dz
where qt′ is the total heat flux through the condensate film. Assuming a linear tempera-
′
ture profile for the condensate film, q′′ can be expressed as
kl (Ti - Tf )
qt′ =
′
(66)
δ
where Ti is the condensate/air interface temperature.
The presence of condensate film can enhance the heat and mass transfer at the conden-
sate-air interface due to increased turbulence and effectiveness roughness. This can be
20



 Previous Page
Previous Page
