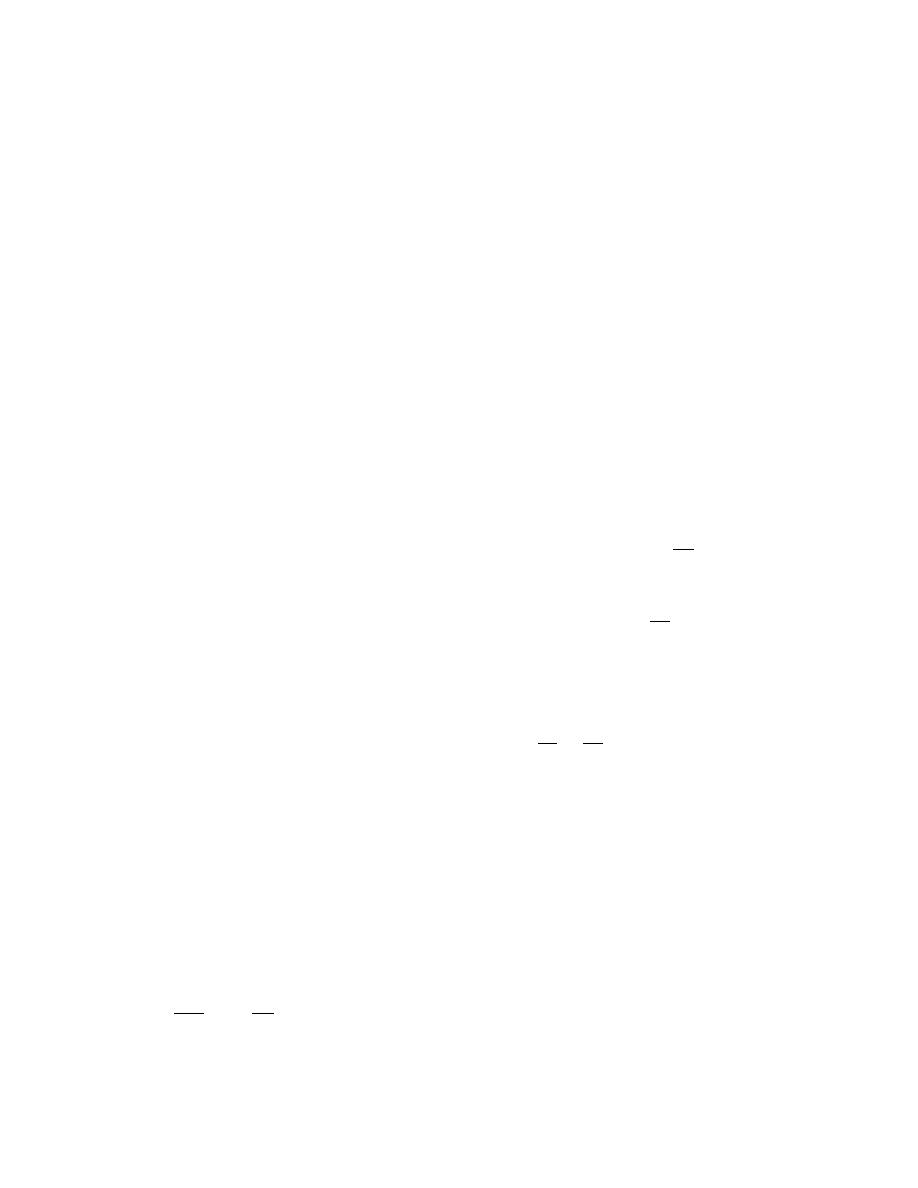
ing variables are known for a given soil. As a first
This relationship introduces the soil function kw,
approximation, the amount of residual unfrozen
the hydraulic conductivity. Each soil will have its
water is assumed to be equal to the lower limit of
unique hydraulic conductivity function. It is not
freezing for the soil. In some situations, this might
a specific property of heaving soils, but is rather a
represent all the required information for the mod-
general material property of all frozen soils, heav-
eler. More often, the heaving pressure, and lens
ing or non-heaving. It must be known in order to
thickness and spacing are also required.
calculate the heaving process.
To date, most efforts to calculate this material
property are by inference. It is inferred from ther-
Second physical approximation
mal analysis (van Loon et al. 1988), back calcula-
(equivalence of instantaneous
tions (Ratkje et al. 1982 ) and unsubstantiated in-
and averaged fluxes)
ference to non-frozen soil (Guymon and Luthin
To calculate the heaving pressure and lens lo-
1974). Black and Miller (1990) were able to directly
cation within the fringe, profiles of temperature
measure the change in hydraulic conductivity in
and pressures must be calculated throughout the
air-free, lens-free and solute-free frozen soil as a
fringe. To perform such calculations, a method of
function of unfrozen water content. Their analy-
executing mass and energy balances within the
sis found that if the measured hydraulic conduc-
fringe must be obtained. This is accomplished with
tivity was expressed a function of the difference
the second physical approximation. It states that
between the ice and water pressures
the instantaneous fluxes of matter and energy at
the beginning and the end of the lensing cycle are
φ = ui - uw
(6)
equal to the averaged values of the fluxes during
the lensing cycle.
then the analogous expression given by Brooks
Another way of stating the second approxima-
and Corey (1964) for partially saturated and ice-
tion is that any instantaneous fluctuations in mag-
free soil could be transformed to
nitude of the mass and energy fluxes during the
α
φb
lensing cycle are negligible. This means that the
W (φ) = (Wsat - Wd )
+ Wd
(7)
magnitude of the penetration rate, heave rate and
φ
temperature gradient within the unfrozen soil are
and
invariant with time and space. In finite difference
β
φb
form, the local mass balance within the fringe is
kw (φ) = (kw )sat
.
(8)
φ
(qw )n+1 = (qw )n + vb
Fourier's law
- Y(vb + vi )[Wn - Wn+1] ,
The flux of thermal energy through the fringe
(3)
b
is assumed to follow the Fourier 's law
and thermal balance is
dθ
q
=- h.
(9)
(qh )n+1 = (qh )n + h [ (Wn - Wn+1) vb
dz
kh
This relationship introduces another soil function,
]
+ (qw )n - (qw )n+1 .
(4)
Just as the hydraulic conductivity, this material
property is also a function of the pressure differ-
The remaining information required to com-
ence between the ice and water pressures. One
plete all calculations are statements for water and
standard expression is the geometric mean formu-
ice pressures, temperature and a criterion for lens
lation of Farouki (1981)
initiation.
W (φ)
(kh )II(φ) .
kh (φ) = (kh )G (kh )W
e
(10)
Darcy's law
The flux of water through the fringe is assumed
to obey Darcy's law
Clapeyron equation
The equilibrium condition between the ice and
q
duw
= fw - w .
water pressures and temperature is given by the
(5)
dz
kw
Clapeyron equation
3




 Previous Page
Previous Page
