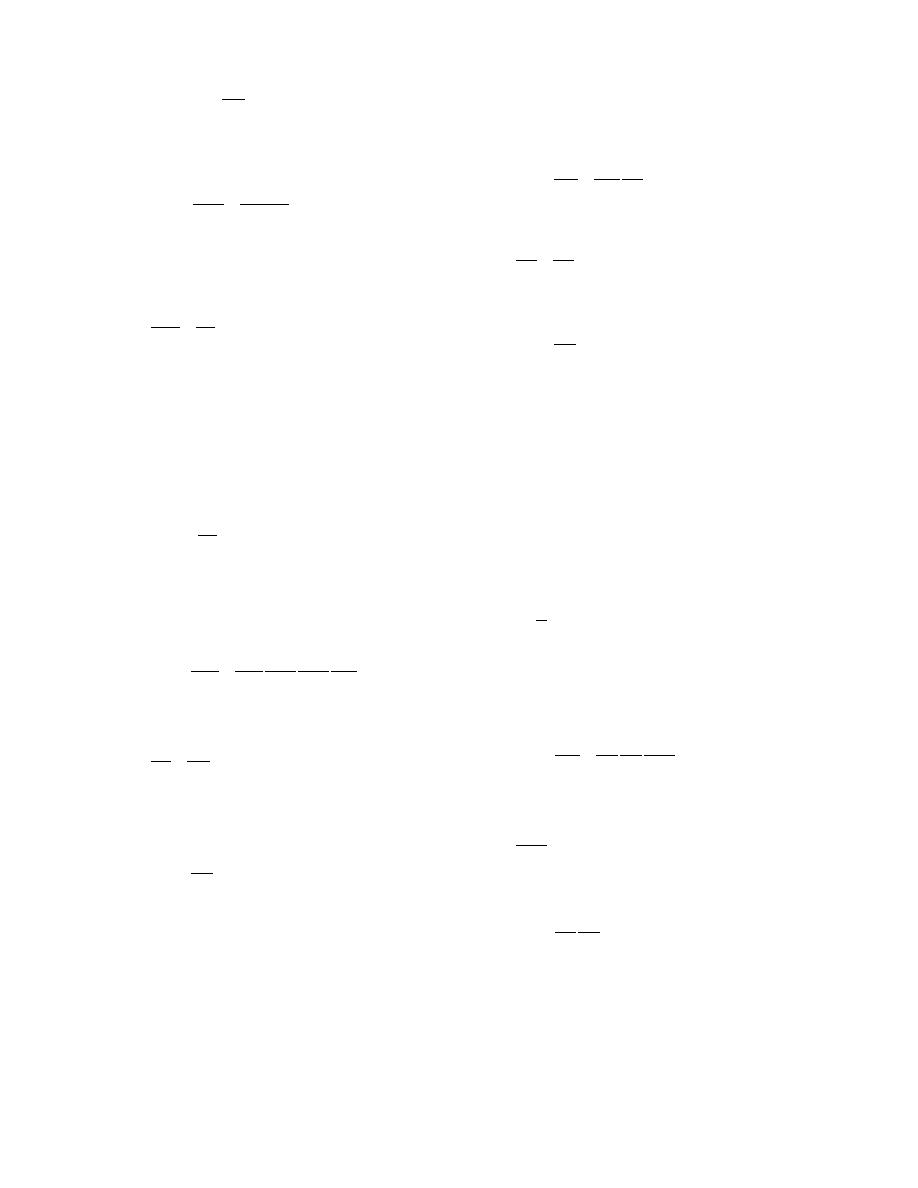
Fi = ma
(A16)
Fm
KF = Kl2 =
.
(A8)
Fp
where a is the acceleration. The model law and
scale factor KFi for the inertia force is
From the definition of weight force, the weight
force model law and scale factor KFw is
Fi m
mm am
KFi =
=
.
(A17)
Fi p
mp ap
mm ag m
Fw m
KFw =
=
= Kl2
(A9)
Fw p
mp ag p
From the definition of acceleration it follows that
Kl
a
= m.
(A18)
Kt2
sidering eq A6, A9 and the relation KF w = KF = K l2
ap
from eq A8,
From eq A6 and A18, eq A17 becomes
ag m
1
=
.
(A10)
Kl4
ag p
Kl
= 2.
KFi
(A19)
Kt
Equation A10 implies that geotechnical model-
Because KFi must equal KF = Kl2 , then
ing requires a technique that elevates the gravi-
tational acceleration of the model.
Kt = Kl .
(A20)
The scale factor for an external force KFe must
satisfy eq A8, and only technical constraints should
That is, the time scale factor is equal to the length
limit this.
scale factor if the inertia force is to be scaled like
A viscous force acting on a small area A can be
the weight force.
defined as
A seepage force can be written as
dv
Fv = s
Fs = iWF
(A21)
(A11)
A
dn
where WF is the weight of the fluid phase and i is
where s is the viscosity of the soil skeleton and
the hydraulic gradient defined by
dv/dn is the velocity gradient. The model law
v
and scale factor for the viscous force KFv can then
i=
(A22)
be written
k
sm dvm dnp Am
in which v is the superficial velocity of the fluid
Fv m
KFv =
=
.
(A12)
and k is Darcy's coefficient of permeability. From
sp dvp dnm Ap
Fv p
eq A21 and A22 the scale factor KFs for the seep-
age force can be written as
From the definition of velocity it follows that
vm kp WFm
Fsm
KFs =
=
Kl vm
.
(A23)
=
.
(A13)
Fsp
vp km WFp
Kt
vp
Equation A8 implies that
From eq A1, A4 and A13 and the fact that viscos-
WFm
ity is independent of gravity, KFv can be written
= KF = Kl2 .
(A24)
WFp
Kl2
KFv =
.
(A14)
Kt
Then, from eq A13 and A24, eq A23 becomes
Because KFv must equal KF = Kl2 , then
Kl3 kp
=
KFs
.
(A25)
Kt km
Kt = 1 .
(A15)
That is, the time scale factor is 1 if the viscous
A general expression for the coefficient of per-
force is to be scaled like the weight force.
meability is (Mitchell 1976)
An inertia force can be written as
12




 Previous Page
Previous Page
