Figure B2. Stress partitioning of ice, water and air

APPENDIX B: SCALING THE RIGIDICE MODEL

APPENDIX B: SCALING THE RIGIDICE MODEL-continue - CR95_090020

CR95_09
Page Navigation
14

pressed by the differential form of the Gibb's re-

and grains G. These volume fractions are related

lationship. It has been shown (Loch 1978, Black

1992) that the Gibb's relationship for monocom-

G + W (uW , uI ) + I(uW , uI ) = 1 .

(B13)

ponent and multicomponent systems contained

within a porous medium that subjects the water

The complete scaled form is simply

to a general body force can be expressed in a sim-

plified Clapeyron equation. When pressures are

G + W (UW , UI ) + I(U W , UI ) = 1 .

(B14)

given in standard gauge pressures u, the Clapey-

ron equation is written as

The criterion for lens initiation is obtained from

the geotechnical concept of effective stress, or the

particle-to-particle contact stress. When this stress

YIW

is zero, the particles no longer remain in contact

in which hIW is the volumetric latent heat of fu-

and an ice lens is able to form. The SnyderTerzaghi

sion (J/m3),YIW is the specific gravity of ice and

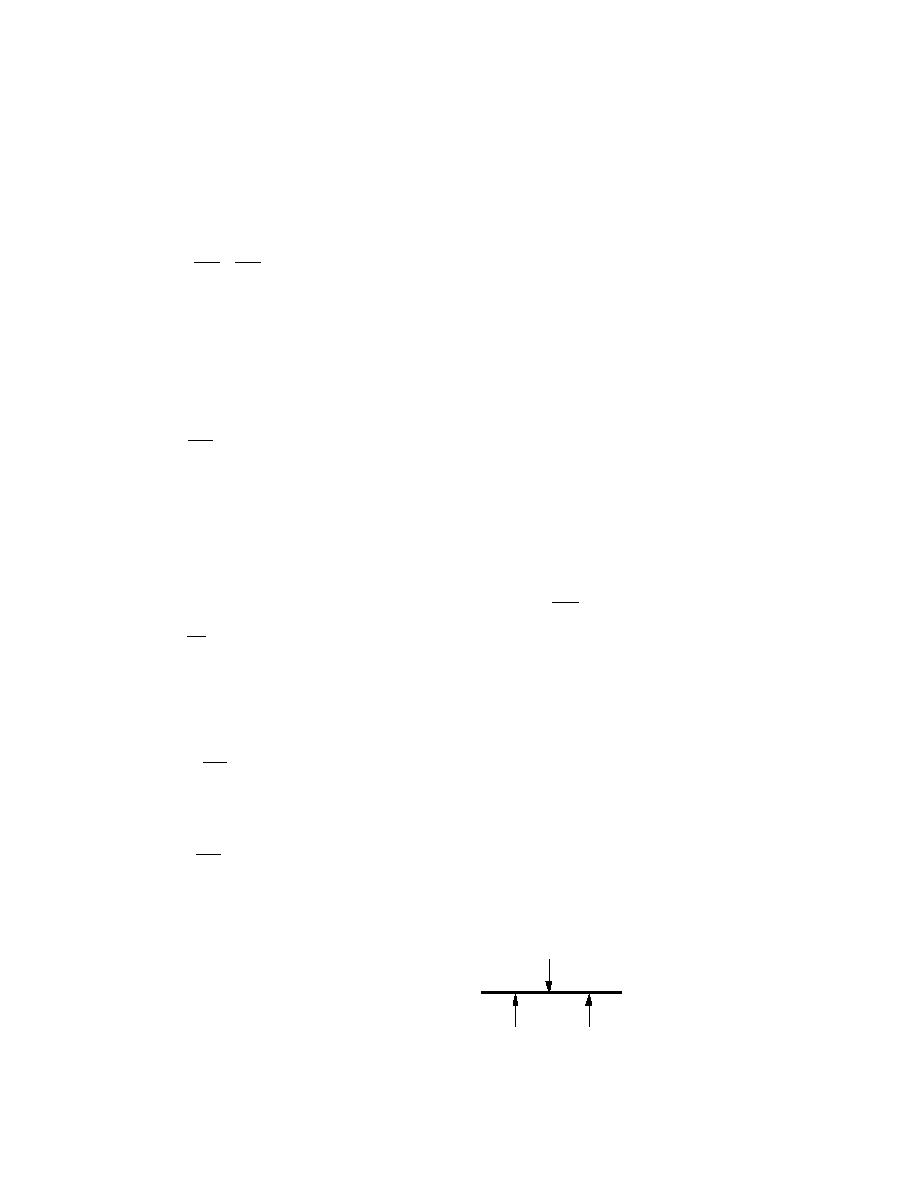
equation partitions the total confining stress σT

θ (C) is the elevation of the melting point of ice

(N/m2) between the effective σe (N/m2) and neu-

from the standard melting point of ice θo. For

tral or pore σn (N/m2) stresses at locations near the

normal water, θ will be negative.

initiation of an ice lens:

The gauge pressures will scale the same as the

Figure B2 shows the partitioning of these stresses.

γ IA

The effective and neutral stresses in this relation-

ship are different from the traditional stresses in

The specific gravity of ice is already dimension-

less, so the remaining constants θo and hIW must

the Terzaghi equation because these include

Snyder 's flawed solid theory (Snyder and Miller

be used to reduced the only variable: tempera-

ture θ. Earlier scaling attempts by Miller (Black

1985). These stresses, like the pressure, take place

at the pore scale, so they will scale just as pres-

1985) developed a reduced temperature that in-

sures do:

cluded the latent heat term, but for the benefit of

clarity, Miller (1990) suggested a different reduced

The flow of water through the frozen fringe is

θo

assumed to obey Darcy's law:

Substituting these scaling parameters for pres-

vW = kW (uW , uI ) ( fW - ∇uW )

sure and temperature into eq B8 results in an ad-

(B17)

ditional reduced term called the reduced latent

heat:

in which vW is the volumetric flux of water

(m3/m2s), kW(uW, uI) is the capillary conductivity

HIW ≡

(m4/Ns), fW is the body force per unit volume

h IW .

(B11)

γ IA

(N/m3) and ∇ is the gradient. To reduce Darcy's

These scaling relationships give a reduced

law we begin by examining the last term. This is

Clapeyron equation:

the gradient of water pressure across the region

of interest. If we are looking at flow through an

UW -

= HIW Θ .

(B12)

individual pore, then this length would appear

YIW

to be λ. This would be correct for this special and

The Laplace and Clapeyron equations show

very limited case. In general, far more complex

that the pressures, temperature and curvature are

flow patterns through a myriad of pore geom-

interrelated. When the porous medium is geo-

etries containing different amounts of ice and

metrically complicated, as in the case of soil, it is

σT

helpful to simplify the pressurescurvature be-

havior by expressing the Laplace equation with

empirically determined material properties. In our

case the necessary material properties are the vol-

Figure B2. Stress partition-

σn

σe

ume fractions for water W(uW, uI), ice I(uW, uI)

ing of ice, water and air.

Index

Privacy Statement
Press Release
Contact