-1
pack as an exponential function as described by
i =
.
(dQsw,x/dx)
Qsw,x
e -x
Qsw,x = Qsw,a
Ice deterioration (melting) is due to the absorp-
tion of internal energy being greater than the com-
bination of loss of energy by conduction to the
at depth x in the snowpack,
free surfaces and convection at the free surface
Qsw,a = flux of shortwave solar radia-
(Fukami and Kojima 1980, Ashton 1984). At
tion absorbed at the snow sur-
Pegasus, about 30 cm of mid-density snow (0.35
face,
= bulk extinction coefficient.
0.45 g/cm3) is adequate to dissipate radiational
heating potential given the boundary conditions
(ambient temperatures, ice temperature at depth,
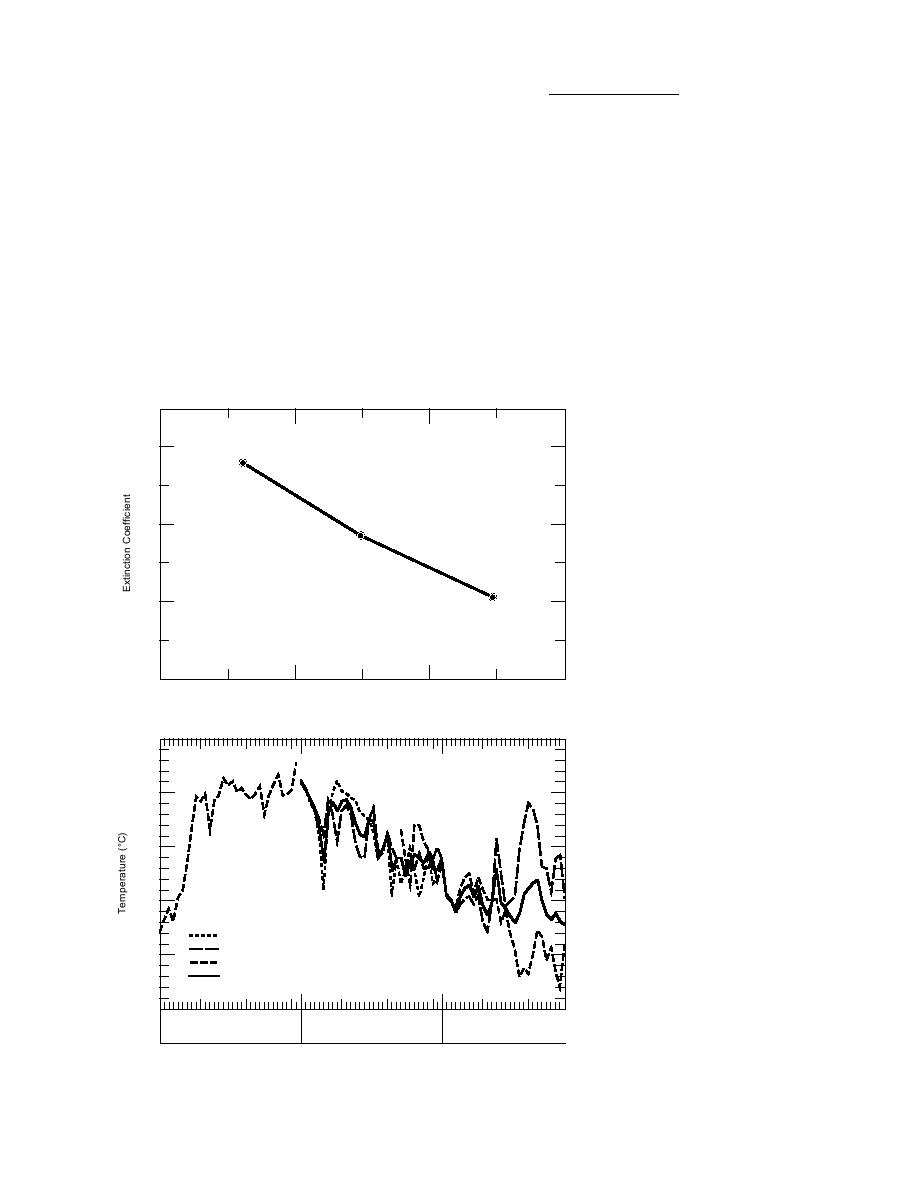
Figure 76 shows the ratio of solar intensity ab-
and angle and duration of solar input).
sorbed at various depth in the snowpack to the
As a simple tool for maintenance personnel at
intensity absorbed at the snow surface as a func-
Pegasus, we used ambient temperature records
tion of snow density by using the following bulk
(Fig. 78) as a basis for decisions about runway
extinction coefficient (Fig. 77), which neglects
protection. By following the trend of the average
spectral dependence:
0.3
0.2
0.1
0
Figure 77. Bulk extinction coef-
0.2
0.3
0.4
0.5
Density (g/cm 3)
ficient for snow.
5
0
5
10
1993
1991
15
1990
1 0
Average
Figure 78. Ambient temperatures
20
recorded at the "Pegasus North"
10
20
30
10
20
30
10
20
Jan
Feb
Dec
AWS.
73



 Previous Page
Previous Page
