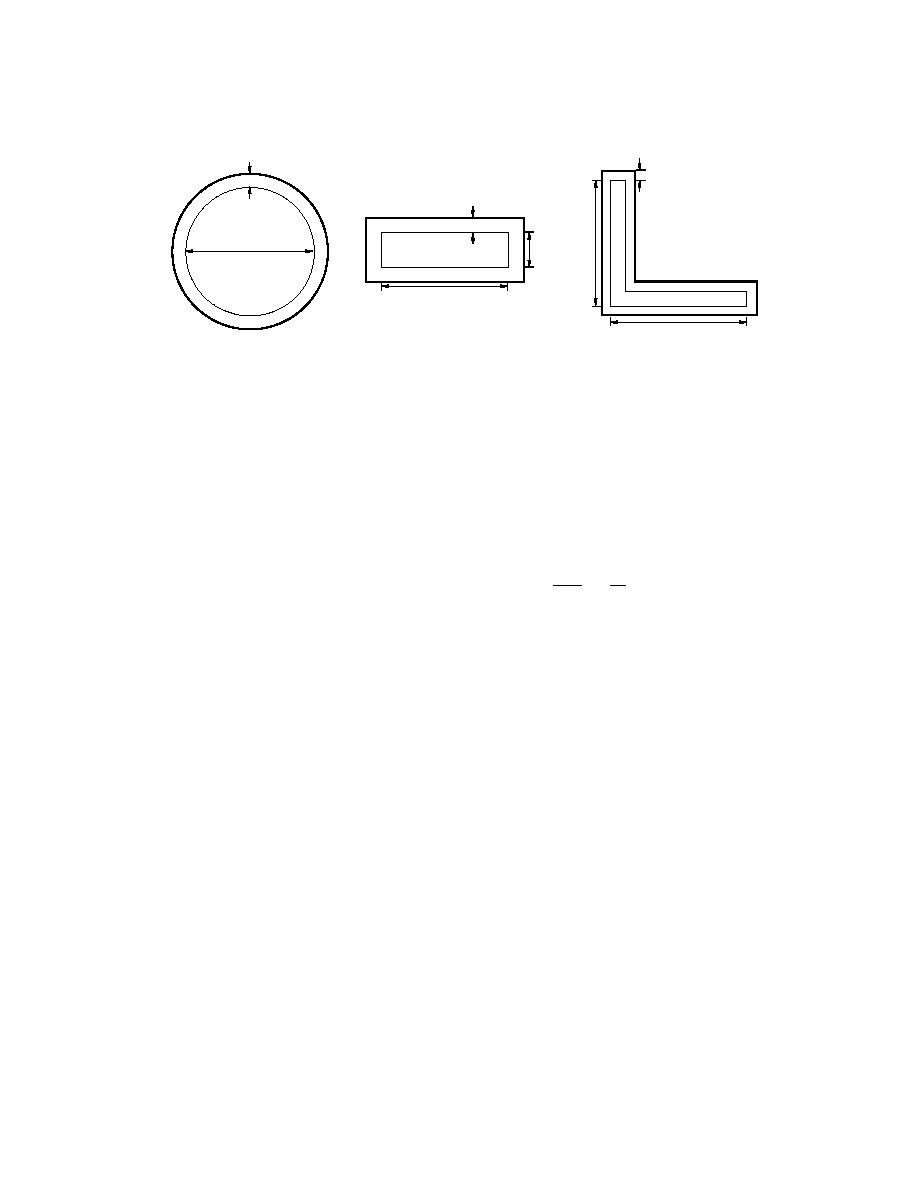
S/D = π
S/D = 2.5
S/D = 4.0
0.28 cm
0.35 cm
0.44 cm
D
D
D/4
D
D
Figure 5. Equivalent uniform radial ice accretions on cylinders with circular, rectangular, and angle
cross sections for a rainfall of 1 cm. The width of the rectangle is 1/4 of its length. The angle has equal-
length legs with arbitrary thickness. The perimeter-to-"diameter" ratio S/D ranges from 3.14 for the
circle to 2.5 for the rectangle and 4 for the angle.
sumed average icicle length as both h and hm are
which intercepts the precipitation. This calcula-
proportional to Lbar1/4. As for the protoicicle, Qw
tion can be generalized to a cylinder with any cross
= 0 and Qs = 0 and the freezing fraction fs is
section to determine the uniform ice thickness on
determined using eq 21. The water that does not
its perimeter:
evaporate or freeze to the sides of the icicle forms
a protoicicle at its tip, and the heat balance for the
Dρo N Pj
Req =
∆t
∑
protoicicle is determined as before. Finally, the
(26)
Sρi j =1 10
water that does not freeze at the tip is assumed to
drip off. The new total icicle mass Mi is distributed
evenly over a cylinder with length Li equal to the
where the summation gives the total precipitation
original icicle length plus the length of the
amount in N hours and S and D are the perimeter
protoicicle.
and horizontal dimension, respectively, of the cross
section. Equivalent uniform ice thicknesses are
shown in Figure 5 for three different cross sections
in a 1-cm rainfall.
6. SIMPLE FLUX MODEL
For many shapes, but not circles, the D/S ratio
The simplest case of ice accreting in freezing
decreases as ice accretes uniformly on the perim-
rain occurs if all the precipitation impinging on the
eter. For those, Req could be determined incremen-
structure freezes in a uniform radial accretion.
tally. When this is done for the rectangle in Figure
When that happens, the amount of ice on the
5, using 0.2-cm increments of rain, the final uni-
structure is directly related to the amount of rain
form radial ice thickness is 0.42 cm rather than 0.44
that falls. For example, if 1 cm of freezing rain falls
cm. This difference is well within the uncertainties
on a 2-cm-wide flat plate and freezes in place, then
in either this simple model or the detailed heat-
a layer of ice 1(ρo/ρi) = 1.1 cm thick results. On a 4-
balance model.
cm-wide plate nearby, the same thickness of ice
This simple precipitation model shows that, at
would form with twice the mass. A 2-cm-diameter
least to first order, the thicknesses of ice on compo-
horizontal circular cylinder intercepts the same
nents with the same shape cross-section but differ-
depth of rain as the 2-cm-wide flat plate. If that
ent diameters are the same. On components with
water depth is then spread uniformly around the
the same diameter but different cross sections, the
cylinder's circumference and frozen, forming a
ice thickness ratio is equal to the inverse of the
uniform radial accretion, then the layer of ice is
perimeter ratio. Thus, uniform radial ice thick-
1(ρo/ρi)/π = 0.35 cm thick. The factor of π is the
nesses determined by this model, or any other
ratio between the circular cylinder's circumfer-
model, for a circular cylinder of any diameter can
ence, over which the ice freezes, and the diameter,
be extrapolated both to cylinders with other cross
13




 Previous Page
Previous Page
