NuD = 0.18 ReD 0.63.
(6)
for smooth cylinders in Morgan (1975). Morgan's
and Achenbach's results and a formula deter-
In these wind-tunnel experiments, the cylinder
mined for smooth cylinders by Zhukauskas and
surface was maintained at a constant temperature.
recommended in Incropera and DeWitt (1985) are
The cylinders were roughened to three different
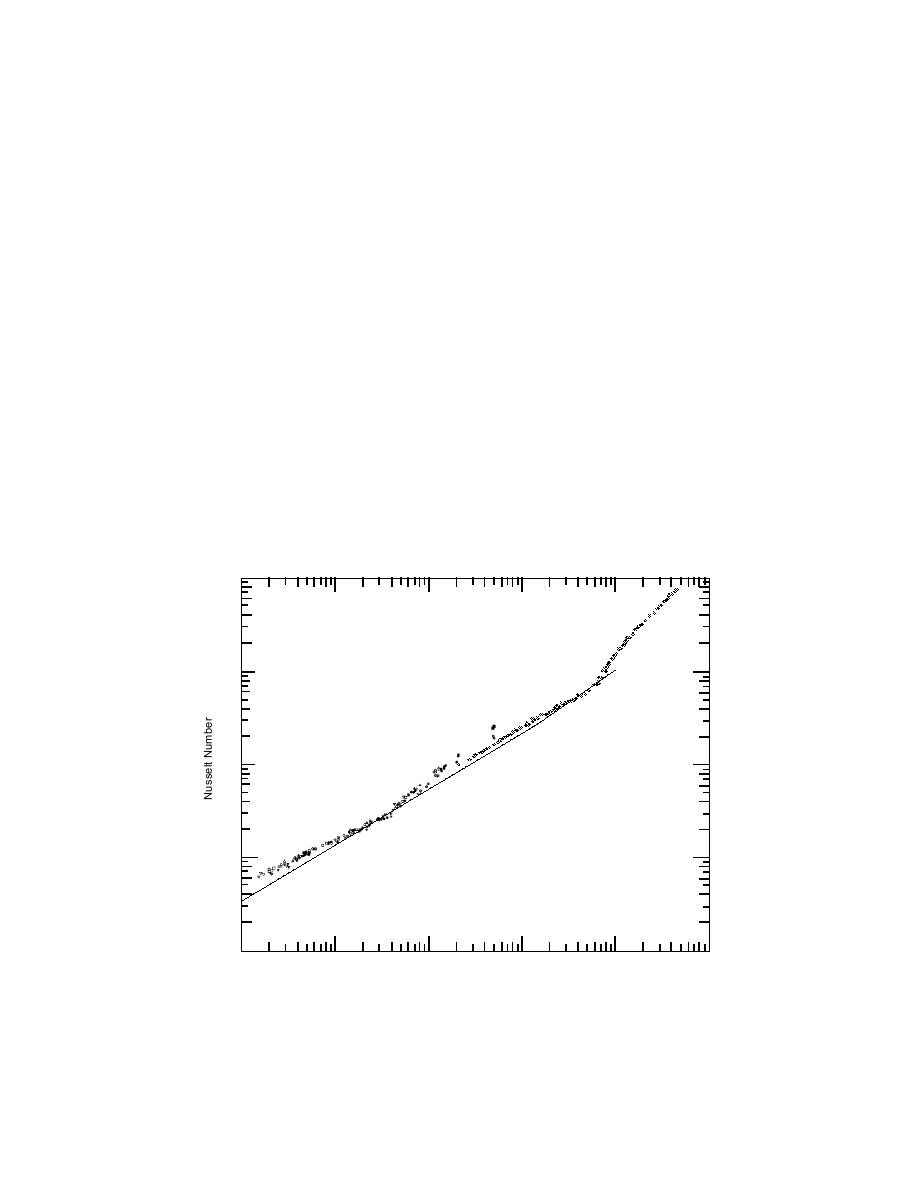
compared in Figure 4. This figure shows that
roughness heights by knurling the surface into
Zhukauskas's smooth cylinder formula predicts
regular pyramidal shapes. The data showed that,
Nusselt numbers that are lower than Morgan's
in subcritical flow, NuD is independent of the
data at low Reynolds numbers and lower than
roughness height, but the upper value of the
Achenbach's at high Reynolds numbers. The scat-
Reynolds number for subcritical flow varies be-
ter of the wind-tunnel data in this figure illustrates
tween 2 105 and 106, decreasing with increasing
the uncertainty in determining the Nusselt num-
roughness. The higher Reynolds numbers for ice
ber for real freezing-rain ice accretions with ir-
accretions in freezing rain are below the upper
regular roughness that is different from that in
value of this subcritical flow range, but the lower
both Achenbach's and Morgan's controlled ex-
values of ReD extend well below 104, the lower
periments. I incorporated Morgan's and
limit in Achenbach's (1977) experiments. To ob-
Achenbach's rough cylinder results in the heat-
tain appropriate Nusselt numbers for these lower
balance model as follows:
Reynolds number conditions, I used results from
NuD = 0.583 ReD0.471 35 < ReD < 1600
Morgan (1973). He determined NuD for bare,
stranded conductors for ReD > 102, maintaining a
NuD = 0.18 ReD0.63
1600 < ReD < 1 106 (7)
6
NuD = 0.00257 ReD0.98 ReD > 1 10 ,
constant heat flux rather than a constant surface
temperature. He compared these stranded con-
ductor results to his Nusselt number formulation
extrapolating Achenbach's formula to lower
10 4
Achenbach
10 3
10 2
Zhukauskas
Morgan
10 1
0
10
10 2
10 3
10 4
10 5
10 6
10 7
Reynolds Number
Figure 4. Nusselt numbers for forced convection over rough and smooth cylinders as
a function of Reynolds number. Rough cylinder data from Achenbach (1977)
are for Reynolds numbers larger than 104. Morgan's (1973) rough cylinder data
are for Reynolds numbers less than 5 104. Zhukauskas's curve (Incropera and DeWitt
1985) is for smooth cylinders for the entire range of Reynolds numbers shown.
8




 Previous Page
Previous Page
