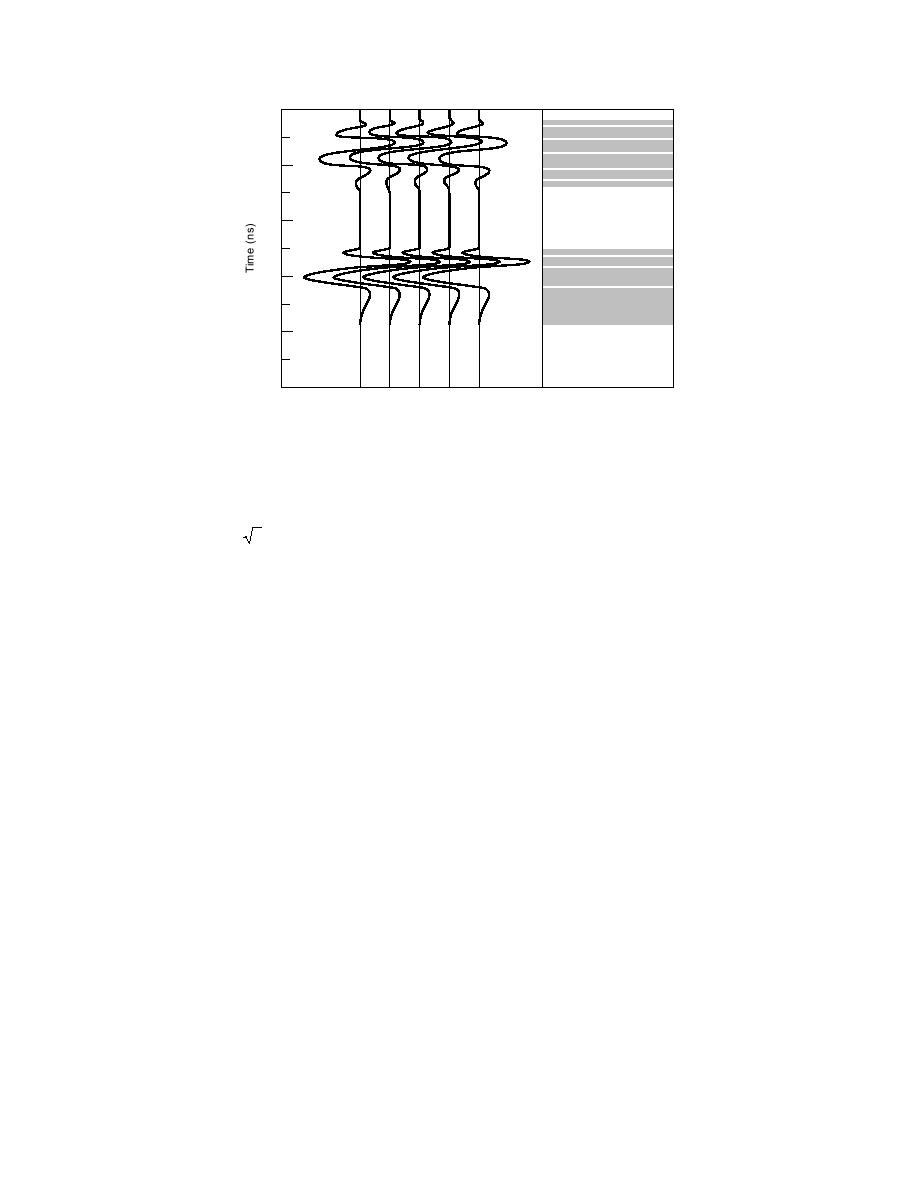
Distance
0
10
20
30
40
50
Figure 4. Wiggle trace display (left) of a series of scans received as the antenna
moves over a short distance, and the equivalent line intensity display.
bolic diffractions with a model hyperbola. The val-
where d is measured in centimeters, t in nano-
ues obtained, calculated at an accuracy of about
seconds and c is the speed of electromagnetic
4%, produced good migrations, as judged by the
waves in a vacuum (30 cm/ns). The quantity n is
often replaced by ε ; where ε = 3.2 for ice and
collapse of the diffraction hyperbolas to a small
area, and can therefore be considered as nearly the
about 1.92.2 for most of the near-surface snow
average refractive index.
encountered. The factor of two in eq 1 accounts
All time section profiles to be migrated had to
for the round trip propagation path of the pulse
be compressed (i.e., stacked, wherein each scan is
and applies only to reflections from horizontal in-
replaced by the average of several scans symmet-
terfaces or to scattering from point sources. Equa-
rically placed about it) so that an adequate migra-
tion 1 can be applied to several layers successive-
tion aperture (number of scans processed at one
ly if n is known for each layer and the time delays
time) could be obtained to cover an entire diffrac-
to each layer interface are easily picked from the
tion. The resulting migration was then stretched
record.
by interpolating between scans to give a reason-
Proper transformation of a standard radar dis-
able ratio between depth and distance scales. De-
tance-vs.-time profile into a more useful spatial
tails of the migration algorithm and the probable
image of distance vs. depth is achieved by a com-
effects of antenna directivity upon it are discussed
putational process known as migration, com-
in Arcone et al. (1995).
monly used in seismic data processing. Migration
Migration is used primarily in the studies of
is not necessary where reflecting horizons gradu-
the dome facilities to help us interpret subsurface
ally change depth with distance, but should be
structure. The diffractions that emanated from the
used where reflections strongly slope or curve
many targets encountered along the proposed
and may be masked by strong diffractions from
tunnel route are not migrated because they them-
local targets.
selves are evidence of target presence (their obscu-
Migration is achieved by many methods. The
ration of snow layering is of no interest) and their
most common, the Kirchhoff diffraction summa-
amplitude and waveforms may supply informa-
tion method (e.g., Yilmaz 1987), is used in these
tion about their material nature.
studies. Migration requires a wave velocity (or
value of n) for each material type encountered,
but we used a one-layer approximation for the
RESULTS AND DISCUSSION
snow; i.e, we assumed that the snow is a homog-
Station site surveys
eneous matrix of constant n and containing em-
The objectives of these surveys were twofold: to
bedded anomalies. In fact, n increases gradually
obtain values for the effective dielectric constant of
with depth. We used a migration refractive index
the firn (i.e., snow over a year old, but not yet com-
5



 Previous Page
Previous Page
