stress on the ice cover. Figure 26 identifies the two layers. Note that α refers to the
area of each respective layer, P is the wetted perimeter, and the subscripts b and i
designate the bed- and ice-affected variables. The dashed line indicates the line of
nominal zero shear or the boundary between the two layers. The total shear force
per unit length of flow area is
τP = τ bPb + τi Pi .
(55)
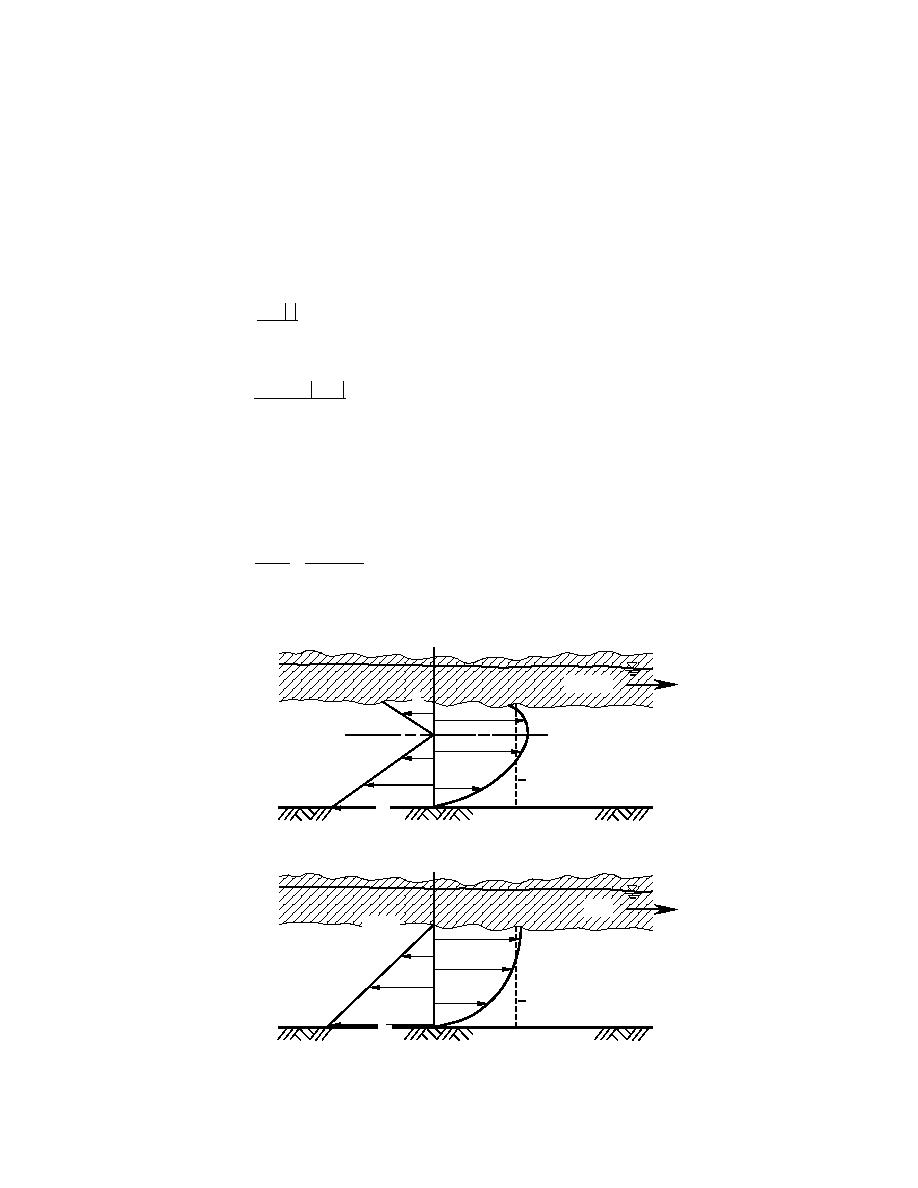
If the "two-layer approach" is valid for any value of ice velocity υ, such as depicted
in Figure 27, then the shear stress at each boundary is expressible as
ρfbu u
τb =
(56)
8
and
ρfi (u - υ) u - υ
τi =
.
(57)
8
The absolute value sign captures directional shear. It can be dropped provided that
stress direction is preserved in the momentum equation.
The "two-layer approach" assumes that each layer can be adequately described
using the Darcy-Weisbach relationship for flow resistance and thus can be related
to the friction slope of the water flow, i.e.
f (u - υ)
2
fbu2
= i
Sf =
.
(58)
8Rb g
8Ri g
0<υ<u
τi
τ=0
u
τb
a)
υ=u
τi = 0
u
τb
b)
Figure 27. Shear stress due to water flow for cases of a moving jam.
35





 Previous Page
Previous Page
