The weight of the cover in the downstream direction f3 can be defined as
u2
f3 = siρgη
(12)
C2RH
where RH is the total hydraulic radius beneath the ice. Substituting eq 11 and 12
into 10, and dividing by H2 (H = the open water depth just upstream of the ice
cover), renders eq 10 dimensionless, i.e.
η
Bu2
η2
2τc η
+ si (1 - si ) 2 .
1 + si
=
(13)
C2 H 2
RH ρgH 2
H
Equation 13 can be used to predict ice thickness for the wide-jam case. Pariset et al.
recognized that freeze-bond forces are of lesser importance for thicker jams, and
are not important during breakup conditions, because jam resistance is dominated
by gravitational effects, i.e., ice weight. They developed a dimensionless stability
parameter X to relate jam thickness to upstream open-water conditions:
2
3
η
η
si (1 - si )
1 - si
H
H
2
2
Bu
Q
X=
= 2o2 =
η
(14)
24
BC H
CH
1 + si
H
where Q is water discharge and uo is bulk open water velocity for uniform flow far
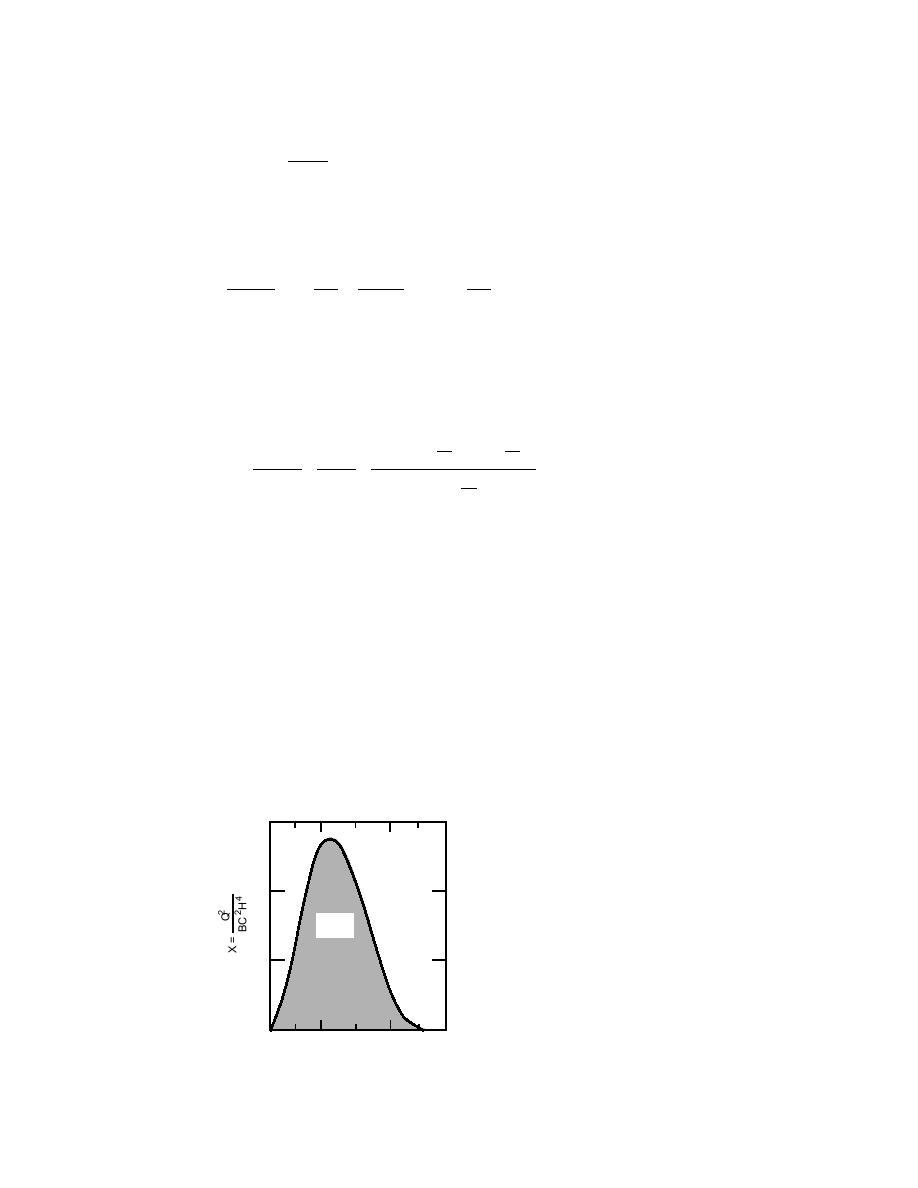
upstream of the jam. Values of X are plotted in Figure 14 for si = 0.92 and = 1.28,
which are values adopted by Pariset et al. for jams in the St. Lawrence River. The
figure indicates jams as being stable (inside the bell curve) or unstable (outside the
curve). The curve is useful, but it does not enable direct calculation of ice thickness.
Moreover, it assumes equilibrium conditions, i.e., steady, uniform flow of water
and uniform ice thickness.
Uzuner and Kennedy (1976) presented a detailed formulation of the time-
dependent differential equations describing the force equilibrium in a static, float-
ing ice jam. Their formulation is
3
3 x 10
2
Figure 14. Dimensionless stability
Unstable
Stable
parameter. (After Pariset et al. 1966.)
Region
Region
1
0
0.4
0.8
1.2
η/H
15





 Previous Page
Previous Page
