0
'
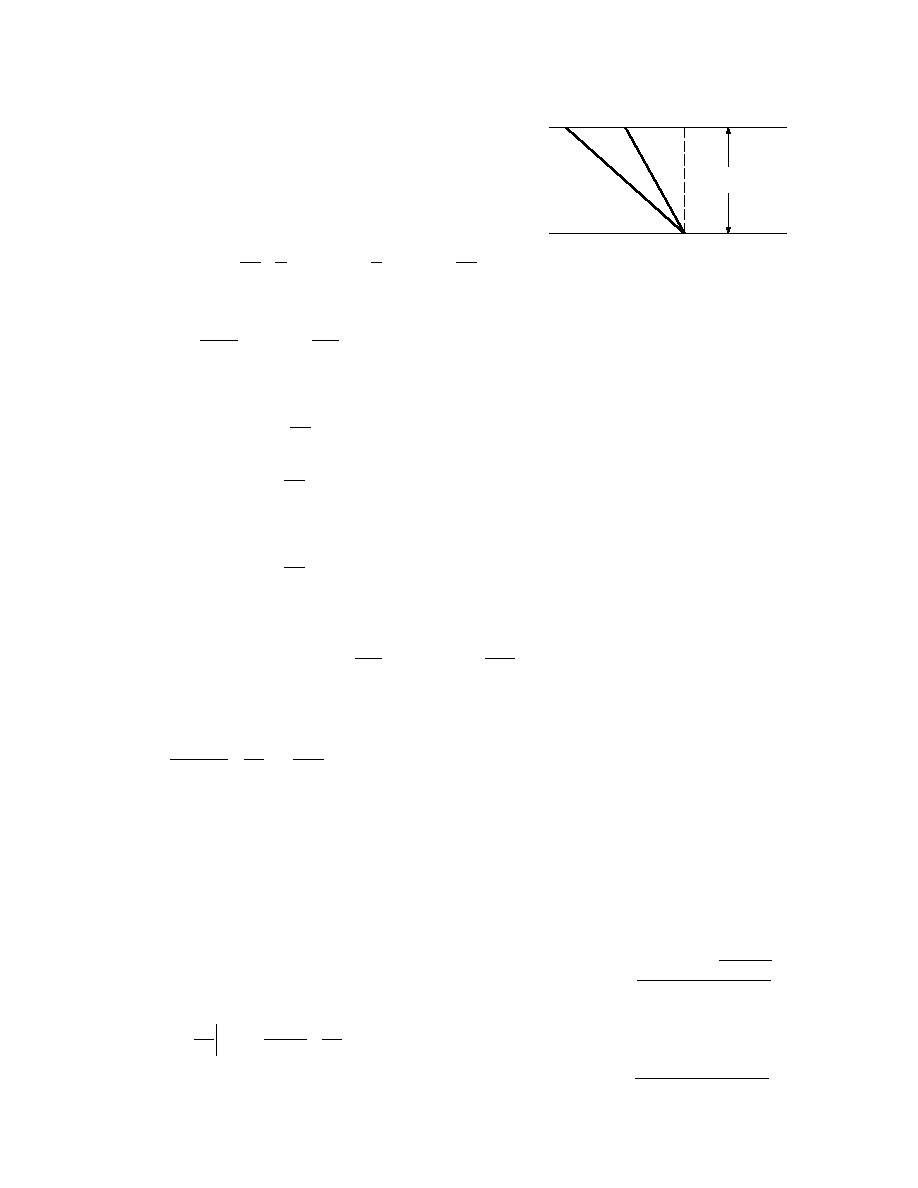
adjusts to its new equilibrium value. Figure D2 sketches the prob-
Ts
Tf
Ts
lem. Obviously, after infinite time the new temperature profile is
t=∞
as shown. However, the temperature will adjust to near the new
equilibrium in a relatively short time. This is a linear problem in
X0
t=0
non-phase-change conduction and has been solved by Lachen-
bruch et al. (1982). The transient temperature is
∞
(
)
1 M
x (D5)
T = Ts′ + (Tf - Ts′)
x
2 o
+ Ts - Ts′ ∑
Figure D2. Permafrost equilibrium tem-
e sin nπ
Xo π
Xo
perature profiles.
n =1 n
where
n2 π2t
2
Xo
M=
tc =
,
.
4α f
4tc
tc is a characteristic time for sensible temperature changes. The equilibrium temperatures are simply
(
) Xxo
To = Tso + Ts - Tso
(D6)
T∞ = Ts′ + (Tf - Ts′)
x
.
(D7)
Xo
The change in sensible heat, going from the state at t = 0 to the state at t = ∞, is
(
) X2o .
Qs ∞ = Cf Ts′ - Tso
(D8)
The change in sensible heat at any time t is
∞
[
]
(
)
Xo
e M
(T - To )dx = Qs ∞ + 2 Ts - Ts′ Xo ∑ 2 1 - (-1)n .
2Cf o
∫
Qs = Cf
(D9)
π
n =1 n
o
Thus, the relative change in sensible heat is
4 ∞ e M
[
]
Qs ∞ - Qs
= 2∑
1 - (-1)n .
(D10)
π n =1 n
2
Qs ∞
Note that this quantity does not depend upon the surface temperatures. The relative change is shown in
Table D2. The sensible heat change attains 93% of its ultimate value at t/λ = 1.0 (t = 1666 years) and 99% at
t/λ = 1.78 (t = 2966 years). The sensible heat changes would be essentially completed after about 1670
years. From this time on, the bottom of the permafrost would slowly melt.
Table D2. Relative change
Change in frozen zone temperature gradient at bottom of permafrost
in sensible heat.
The time required for the temperature gradient, in the frozen zone, to
change is important since this quantity will determine the rate of change of the
Qs ∞ - Qs
t/λ
permafrost bottom depth. The gradient at the depth Xo can be found from eq
Qs ∞
D5 and is
0.25
0.438
0.50
0.236
∞
Tf - Ts′ 2
1.0
0.069
(
)
T
Tso - Ts′ ∑ (-1)n e M .
+
δ=
=
(D11)
1.50
0.020
x = Xo
x
Xo
Xo
n =1
1.78
0.010
2.0
0.006
36





 Previous Page
Previous Page
