APPENDIX B: QUATERNARY CYCLIC THERMAL MODULATION
Thaw process
Assuming that melting occurs with a fraction f of the geothermal heat flow going into increasing the sen-
sible heat allows an estimate to be made of the thaw time and the final temperature, noted in Figure 12,
which will then be the initial temperature distribution for the next freeze cycle. Referring to Figure 11, we
assume that the fraction of geothermal energy available for melt at any time is
( fm - 1)X + Xo
f=
(B1)
Xo
where fm is the melt fraction at the conclusion of melt and Xo is the initial frozen thickness. The tempera-
ture in the region of changing temperature is
T2 = Tf + b(x ∆1) + c(x ∆1)2
(B2)
where ∆1 = Xo X and b,c are functions of time only. The initial temperature of the soil is
x ≤ Xo
Tf
Ti =
.
(B3)
Tf + G( x - Xo )
x ≥ Xo
The sensible heat added to the soil is
Xo +δ
Xo
∫ (T2 - Ti )dx + Cu ∫ (T2 - Ti )dx.
Qs = Cu
(B4)
Xo -X
Xo
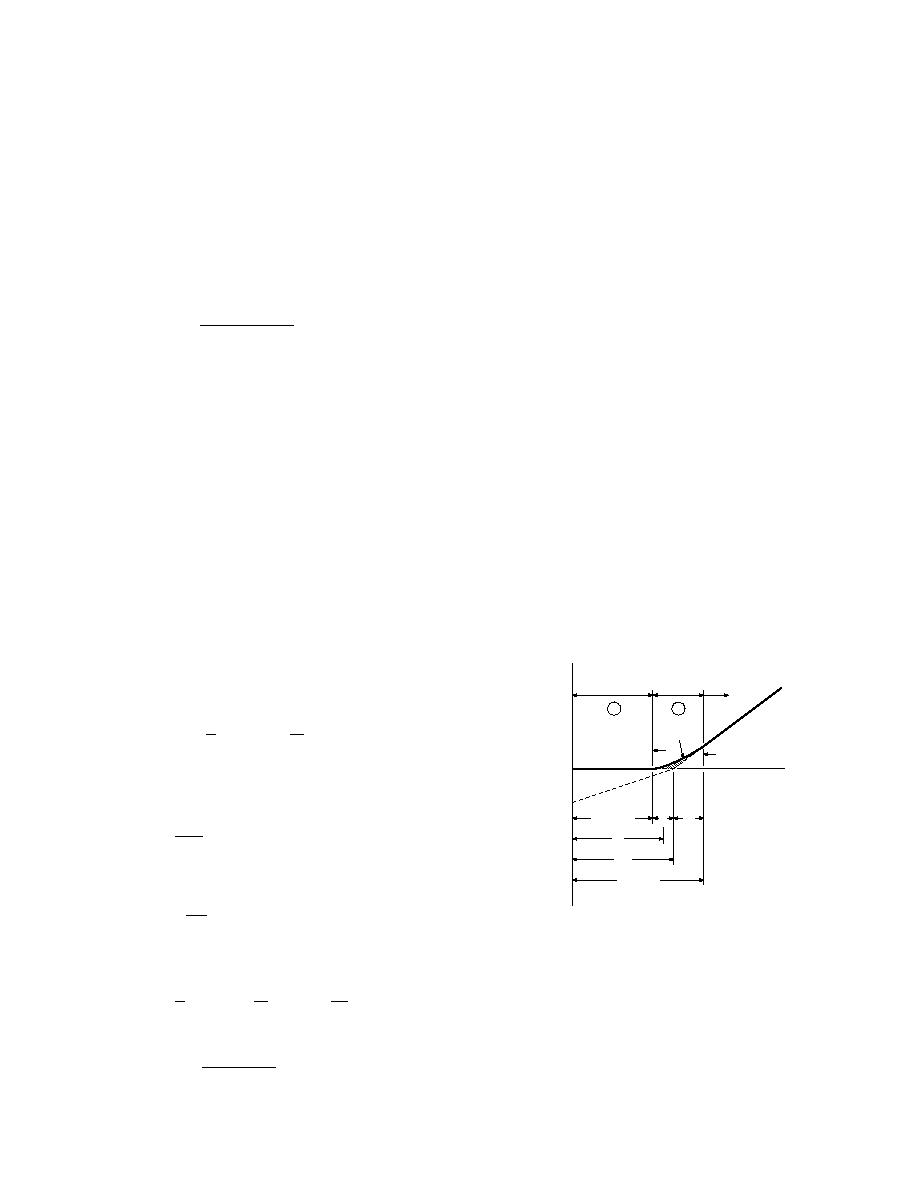
The sensible heat addition is shown as the shaded region of Figure
Changing
Temp.
Frozen
Thawed
B1. The sensible heat at any instant is then
2
1
G Cu X δ - .
X
1
Qs =
T2 (x, t)
(B5)
2
3
q1
qg
Tf
The change in sensible heat must equal the fraction of the geother-
mal energy not used for melting, or
Ts
δ
(Xo X)
X
dQS
= qg (1 - f ) .
(B6)
x
dt
Xo
The energy balance at the melt interface is
(Xo + δ)
dX
= fqg .
L
(B7)
x=0
dt
Figure B1. Bottom melt process.
The solutions to these equations lead to
(
)
GCu X δ - = qg t +
1 - e Mt
X
1
1
(B8)
M
2
3
(
)
Xo 1 - e Mt
X=
(B9)
(1 - fm )
25





 Previous Page
Previous Page
