EM 1110-2-2907
1 October 2003
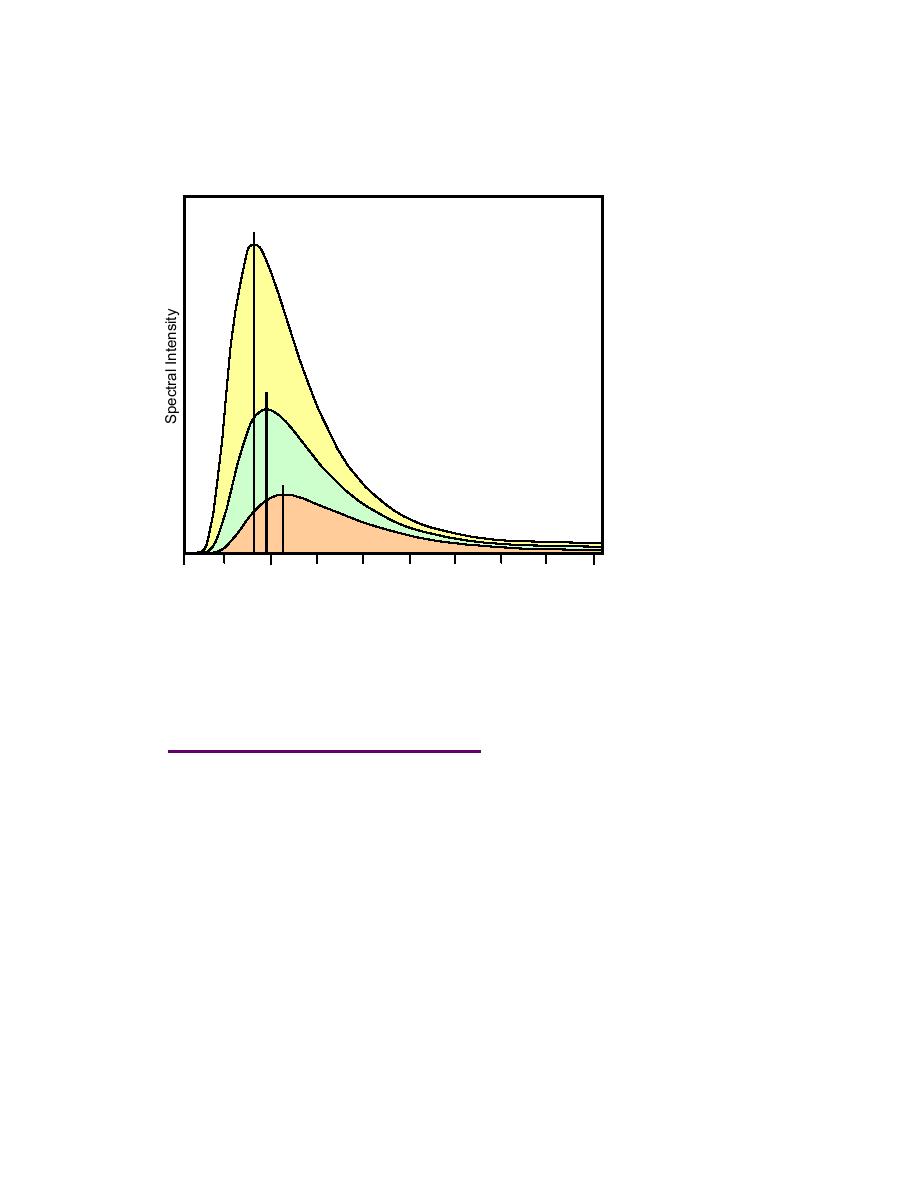
This simply means that the total energy emitted from an object rapidly increases with
only slight increases in temperature. Therefore, a hotter black body emits more radiation
at each wavelength than a cooler one (Figure 2-10).
Yellow = 6000 K
Green = 5000K
Brown = 4000 K
0
1000
2000
3000
4000
Wavelength (λ) nm
Figure 2-10. Spectral intensity of different emitted tempera-
tures. The horizontal axis is wavelength in nm and the verti-
cal axis is spectral intensity. The vertical bars denote the
peak intensity for the temperatures presented. These peaks
indicate a shift toward higher energies (lower wavelengths)
with
increasing
temperatures.
Modified
from
(3) Summary. Together, the Wien and Stefan-Boltzmann Laws are powerful tools.
From these equations, temperature and radiant energy can be determined from an object's
emitted radiation. For example, ocean water temperature distribution can be mapped by
measuring the emitted radiation; discrete temperatures over a forest canopy can be de-
tected; and surface temperatures of distant solar system objects can be estimated.
k. The Sun and Earth as Black Bodies. The Sun's surface temperature is 5800 K; at
that temperature much of the energy is radiated as visible light (Figure 2-11). We can
therefore see much of the spectra emitted from the sun. Scientists speculate the human
eye has evolved to take advantage of the portion of the electromagnetic spectrum most
readily available (i.e., sunlight). Also, note from the figure the Earth's emitted radiation
peaks between 6 to 16 m; to "see" these wavelengths one must use a remote sensing
detector.
2-13



 Previous Page
Previous Page
