be of far greater importance than the last param-
Q, and by specifying that ice floats. The influence
of water viscosity ν can be neglected if it is as-
eters in eq 9. Only when the outflow channel is
comparatively shallow or rough will the last
sumed that flow in the channels and around ice
parameters be important.
pieces is fully turbulent. For ice pieces in actual
rivers, surface tension σ is negligible. The num-
The effects of viscosity and surface tension
ber of variables finally reduces to 19.
become important when conducting hydraulic
If the inflows and outflow of ice occur as a single
model tests using small pieces of model ice for
layer of ice pieces of a given size conveyed in sub-
simulating ice movement. Then, eq 9 should be
critical flow conditions, the following functional
expanded to include values of Reynolds number
QD/(νbY) and Weber number ρLQ2/(bY)2σ for the
relationship may be written for the areal concen-
tration of ice discharge on the confluence outflow
channels.
channel Cc, as the dependent variable of interest:
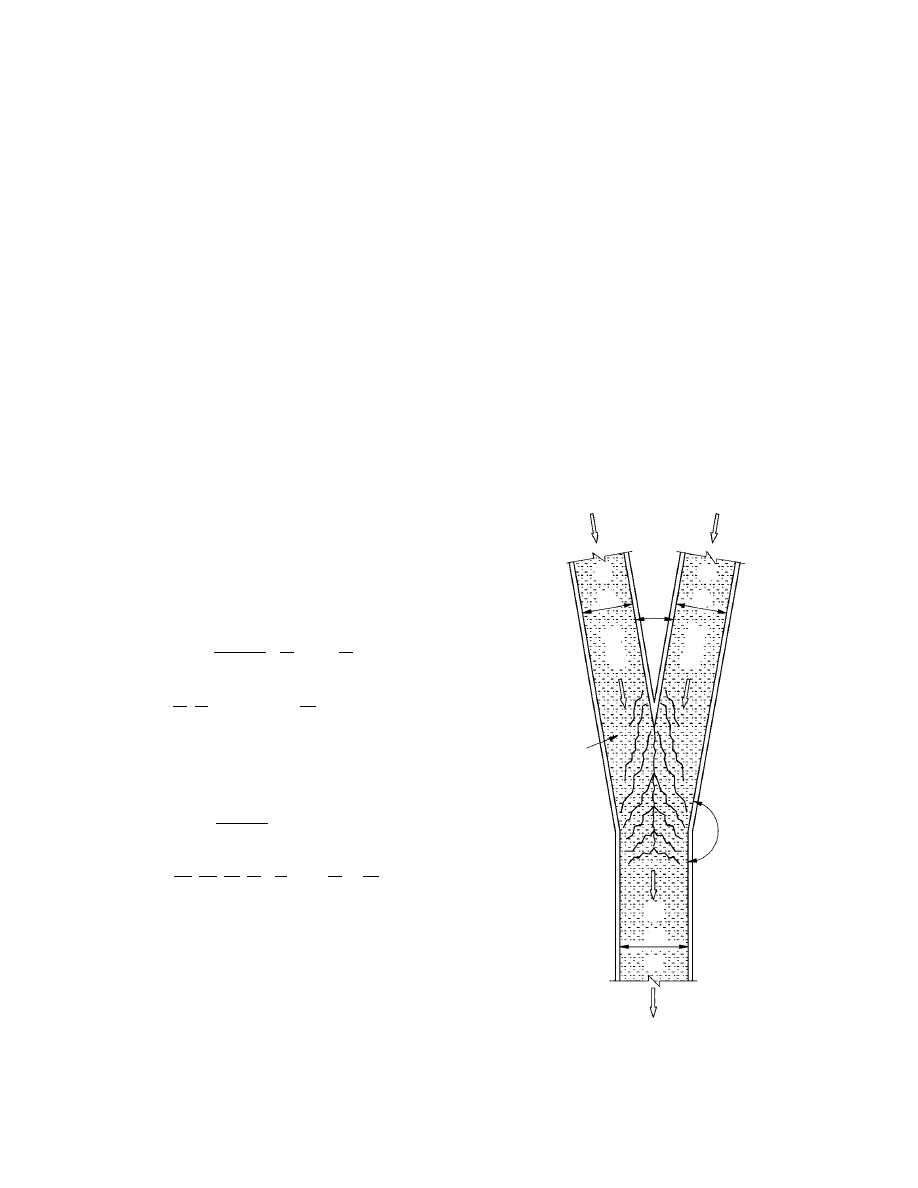
Ice-layer movement through a confluence
Cc = fd (Q1 , Q2 , b1 , b2 , bc , Y1 , Y2 , Yc , k, D, h,
Flow in a single channel with a moving ice cover
, C1 , C2 , α, β, , ρ, ρi ) .
(7)
(Fig. 4) can be defined using its discharge Q and
depth Y, width b, channel roughness k, and ice
Equation 7 assumes that, for a confluence of riv-
roughness ki. The volumetric rate of ice-accumu-
ers, Qc = Q1 + Q2, and for a confluence of a river
lation discharge as a contiguous layer of ice ex-
and a reservoir or lake, Q2, G2 = 0, and eq 5 and 6
tending across the full width of the channel and
pertain. The 19 variables in eq 7 are reducible to
moving at a speed less than the surface water
16 nondimensional parameters, given two basic
speed in a single channel can be written as a volu-
metric proportion η of the water discharge bulked
dimensions (length and time) involved with the
volumetric discharge of ice through a confluence.
Q1
Q2
If a dimensional analysis is carried out using D,
Q1 + Q2, and ρ as the repeating variables, the fol-
lowing functional relationship emerges for the lim-
Y1
Y2
iting condition of a single layer of free-drifting ice
b1
b2
discharging through a confluence:
a
h2
h1
Q1
b
Y
Cc = ϕdl
,
,
,
H2
H1
Q1 + Q2 D 1,2,c D 1,2,c
ρ
k h
, , C1 , C2 , α, β, , i .
,
(8)
ρ
D D
Moving layer
Equation 8 can be rearranged to relate channel
of ice
widths in a more meaningful manner:
Q1
Cc = ϕd2
, C1 , C2 , α, β,
Q1 + Q2
b
ρ
b b b D h
k
, , , i .
, 1 , 2 , c , ,
(9)
bC bC D h Y 1,2,C D
ρ
hc
These parameters are useful for describing vari-
bc
ous confluence conditions. For example, in the
simple case of a single channel entering a lake (Fig.
Yc
1d), b1/bc ≈ 0, b2/bc = 1, β = 180, and Q1/(Q1 +
Q2) ≈ 1. Note that eq 8 and 9 can be made more
Qc
elaborate by including additional variables, such
as different ice piece sizes and roughness condi-
Figure 4. Variables influencing
tions in the two confluent channels. For most
ice-layer movement through a
confluences, the first nine parameters usually will
confluence.
5




 Previous Page
Previous Page
