GROWTH OF ICE LAYERS
We will seek solutions in which Vo = 0. In this case eq P1 through P4 are reduced to
f (ξ) = fo , 0 < ξ < δ
(48)
f (ξ) = -K1{T(ξ)}P′(ξ) + K2 {T(ξ)}(α o / η) ,
0<ξ<δ
(49)
T ′(ξ) = -(α o / η)
(50)
k1α1 - koα o = Lfo .
(51)
The left-hand side of eq 51 is the rate of heat removal from the frozen fringe that must be
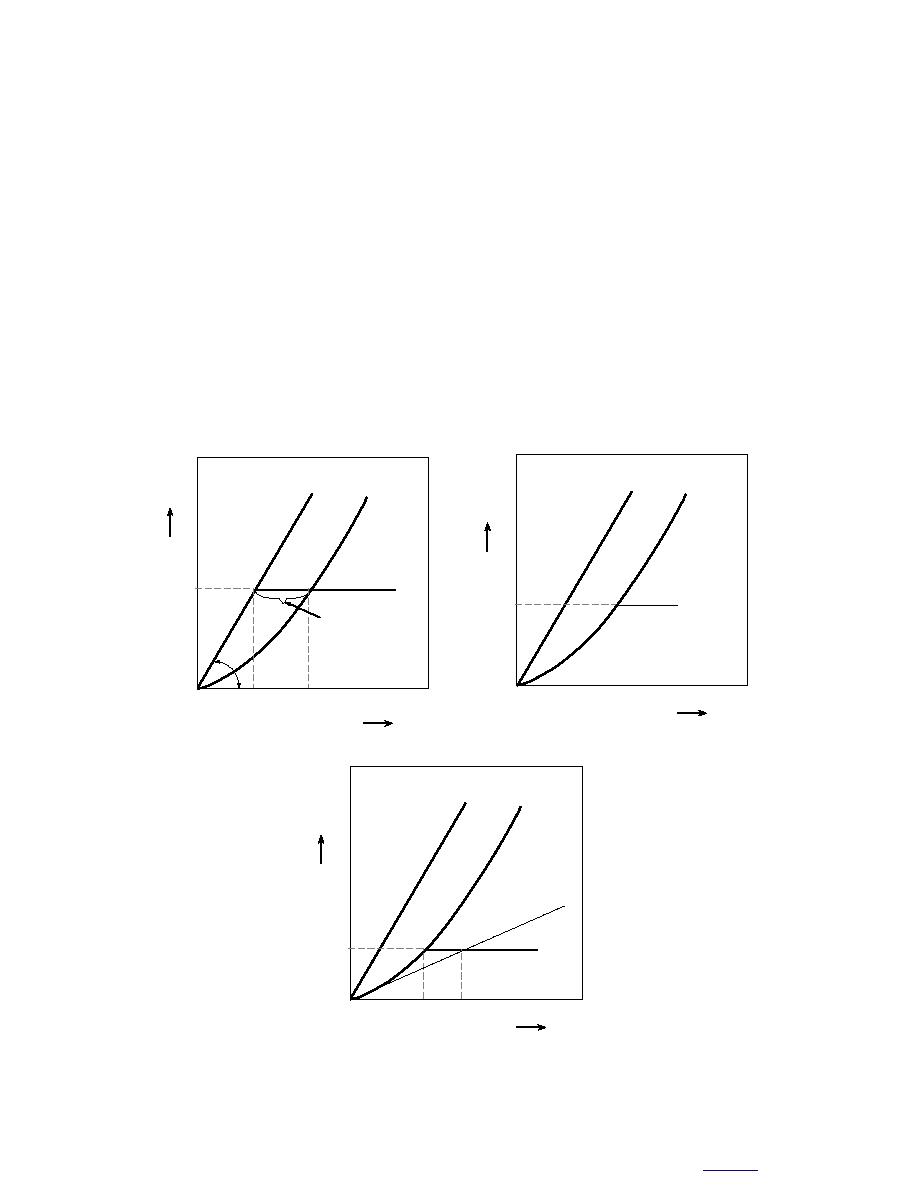
positive during soil freezing. Hence, fo > 0. We will consider a quadrant S = [(α1, αo): α1 ≥ 0,
αo ≥ 0], where we draw a straight line Le starting from the origin (Fig. 2a) defined as
Le = {(α1 , α o ):α o = (k1 / ko )α1}.
(52)
Le
Le
Cs
Cs
Si
αo
Sp
Sm
Si
αo
S+(eo>0)
p
^
αo
L
αoc
Lc(eo=0)
^
l(αo)
-
Sp(eo<0)
Sf
α1e
α1s
0
0
α1
α1
b. Region of frost penetration when σ < σc.
a. Stable growth region of an ice layer.
Le
Cs
Spp(ƒo >0)
αo
Lp(ƒo = 0)
L+
Sx (ƒ0<0)
α1p
α1s
0
α1
c. Region of frost penetration when σ ≥ σc
Figure 2. Temperature gradients α1 and αo.
9
Contents
Previous Page
