depending only on lower-order kinematic waves, the subcharacteristics of eq 7. More gen-
erally both these wave types occur together, with small disturbances traveling along the
characteristics and the primary mass of the flow moving along the subcharacteristics.
The same procedure used in the development of eq 7 can be repeated with eq 6 replacing
eq 5, yielding
φt + ck φx = D φxx
(11)
where D = c0 η = v0 y0 / 2S0 is a noninertial diffusion coefficient. We call this parabolic ad-
2
vective-diffusion equation the linear diffusion wave equation. The dynamic wave celerities
that appear explicitly in eq 7 depend on flow inertia, and are absent from eq 11. The
Hayami (1951) solution of eq 11 is presented in Henderson (1966). Ferrick et al. (1984) de-
veloped an equation from eq 7 with the same form as eq 11 that included higher-order x-
derivatives. The presence of the inertia terms resulted in an inertial diffusion coefficient
that depends on the Froude number F0 = v0/c0:
D = c0 η(1 - F02 / 4).
2
(12)
Dooge (1973), Whitham (1974) and Menendez (1993) also obtained this inertial diffusion
coefficient using different methods.
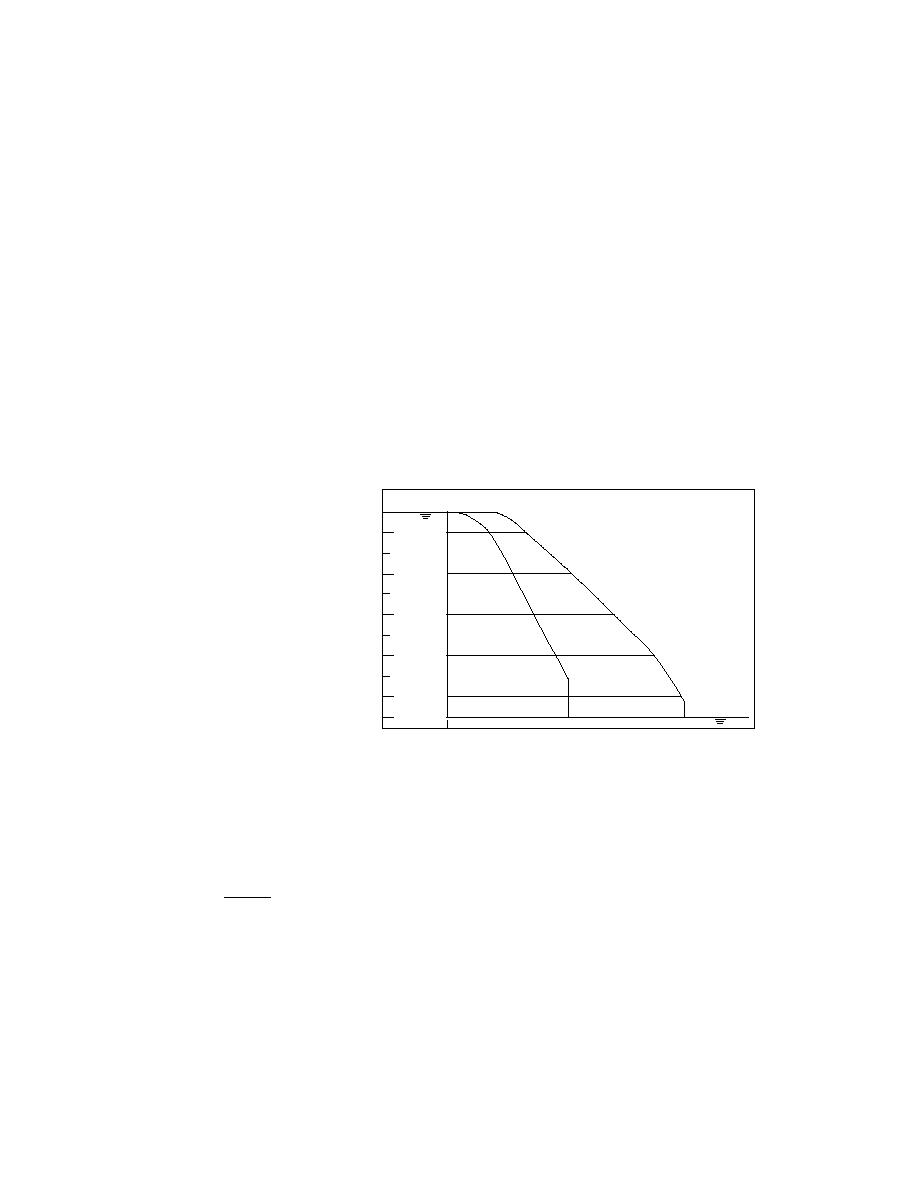
SOLUTIONS FOR LINEAR
∆
1.0
DYNAMIC AND LINEAR
0.9
DIFFUSION WAVES
We will examine the
0.7
linear dynamic wave and
t = ∆t
t = 2∆t
t=0
diffusion wave solutions φ
0.5
for an instantaneous in-
crease between steady
states φ0 and φf at the up-
0.3
stream boundary (x = 0)
0.1
at t = 0. Before this in-
∆
crease, steady-uniform
0.0
flow conditions down-
0
X (km)
stream at φ0 are assumed.
Figure 1. Initial and upstream boundary conditions of the linear equa-
This initial shock maxi-
tions, and dimensionless φ profile development with dimensional dis-
mizes the importance of
tance and time.
inertia, the difference be-
tween the dynamic wave and diffusion wave models. The solutions φ(x,t) are required for
~
positive x and t, and for simplicity we define dimensionless φ as
~ φ - φ0
φ=
(13)
φf - φ0
with φ = 1 at the upstream boundary and a solution interval of zero to one. In the remain-
~
der of this report we drop the tilde, but dimensionless φ is implied. Dimensional (x,t) and
dimensionless φ are used in Figure 1 to depict the initial and upstream boundary condi-
tions, and profile and shock development. Lines that trace the motion of constant φ profile
points, and profile celerity differences between these points, related to diffusion of the pro-
file, are indicated. Nonlinear wave steepening that opposes diffusion can cause a shock to
be sustained, but it is not present here. As a result, the imposed shock attenuates and the
profile separating the steady states elongates with time and distance.
4



 Previous Page
Previous Page
