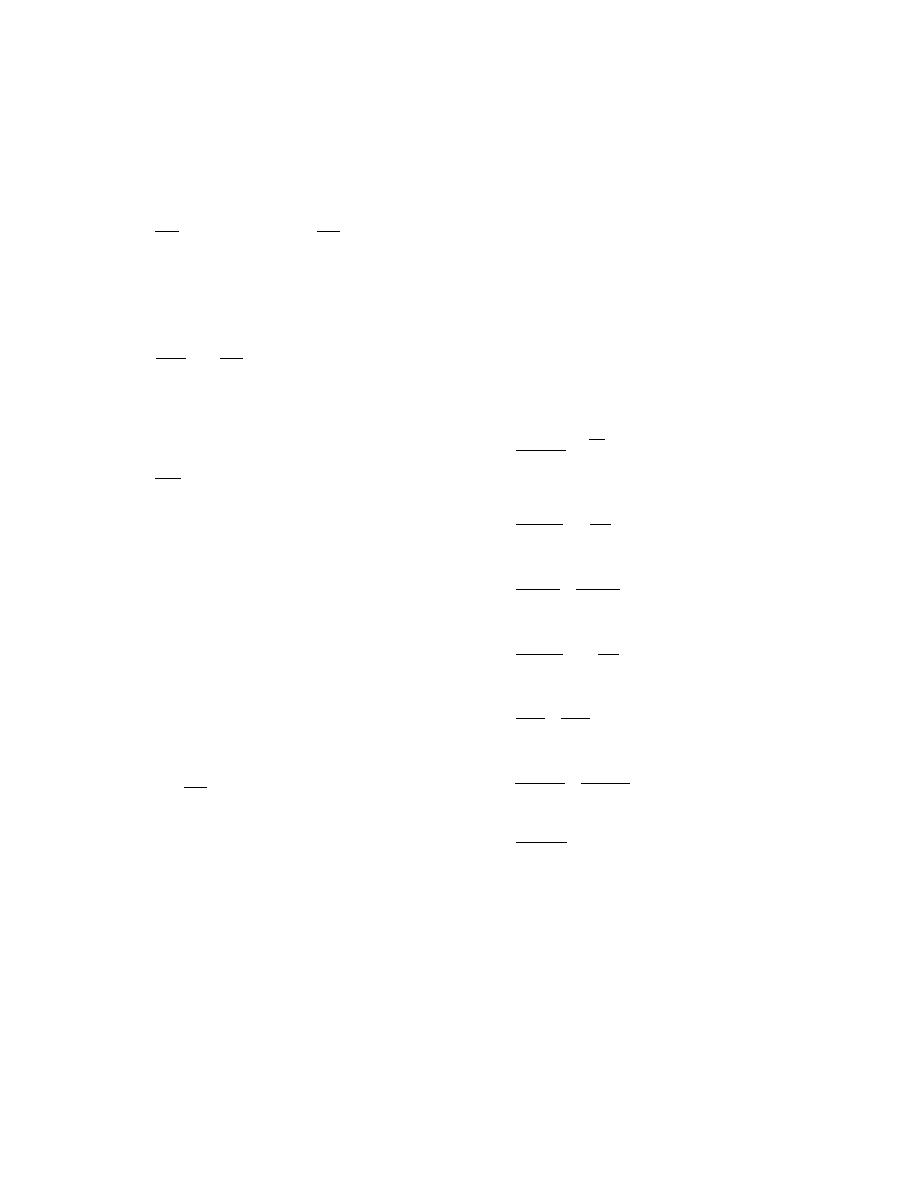
by Pitzer's routine at every iteration. Because of
The conditions of extremum of the Lagrangian
function are found where all first partial deriv-
this it was very difficult to reach the required pre-
atives with respect to components and to
cision of solution (0.1%), even when special steps
Lagrangian multipliers are equal to zero. This
were undertaken.
gives
Another approach is to solve the whole system
of P M + J + 1 equations (eq 4 a,b,c) iteratively by
Φ
nj
Newton's method for nj, nw, and λk. This algo-
= ( 0 + ln 55.51) + ln(
γ j)
j
rithm has been described in detail by Harvie et al.
nj
nw
(1987). It has been successfully applied by Spen-
cer et al. (1990) for strong electrolyte solution
M
P
-∑
- ∑ λ i aij = 0
0 akj
(4a)
modeling, but a working version of the program
k
k =1
i = M +1
has not been published. This algorithm also was
applied by Mironenko (1983) for modeling fluid-
Φ
nj
M
rock interactions during hydrothermal uranium
- ∑ 0 akw
= -φ
k
ore formation.
nw
nw k =1
The second partial derivatives of the Lagran-
gian function are equal to
P
∑ λ i aiw = 0
-
(4b)
1 , if j = j1
i = M +1
Φ
2
= nj
n j n j1
Φ
J
0, if j ≠ j1
= Bi - ∑ aijnj - aiwnw = 0 .
(4c)
λi
j =1
Φ
2
1
=-
There are different approaches to searching the
nj nw
nw
Lagrangian function extremum. One of them is
the algorithm developed by White (1958, 1967)
Φ
Φ
2
2
for homogeneous gas systems, which has been
=
= -aij
nj λ i
λ i nj
further developed for heterogeneous multiphase
systems by Karpov (1976). This algorithm was
applied by the senior author of this report for
Φ
2
1
= -φ
computation of a wide range of chemical equilib-
nw nj
nw
ria (Mironenko 1991, 1992) and is build into the
DiaNIK system (Khodakovsky 1992). The idea of
Φ ∑ nj
the method, as applied to the system under con-
2
= 2 φ
sideration, is as follows. Equation 4a may be
2
nw
nw
solved with respect to nj:
Φ
Φ
2
2
M
P
n
=
= -aiw
nj = w exp ∑ 0 aij + ∑ λ i aij - 0 .
(5)
nw λ i
λ i nw
k
j
γj
k =1
i = M +1
Φ
2
Substitution of these terms into eq 4b and c gives
= 0.
λ i λ i1
the system of P M + 1 equations, which may be
r
solved by Newton's method for λ and nw . The
advantages of this approach are a fast rate of
This matrix of second partial derivatives is
computation, due to a small amount of variables
known as the Hessian matrix.
(their amount does not depend on the number of
Activity coefficients of species and the osmotic
species), and the lack of necessity to undertake
coefficient are calculated at every iteration using
special steps to calculate species at very low con-
Pitzer 's model (Pitzer 1987). In FREZCHEM2, the
centrations or to correct negative values of mass
Pitzer routines published by Marion and Grant
for species during iterations. Unfortunately,
(1994) were used, with insignificant changes
attempts to apply this approach to brine systems
dealing mainly with the interface with data files.
in combination with Pitzer's routine have dem-
The molal amounts of solids are calculated
onstrated that the algorithm is not tolerant of os-
after a local equilibrium has been achieved using
cillations of activity coefficient values, provided
eq 2a.
3




 Previous Page
Previous Page
