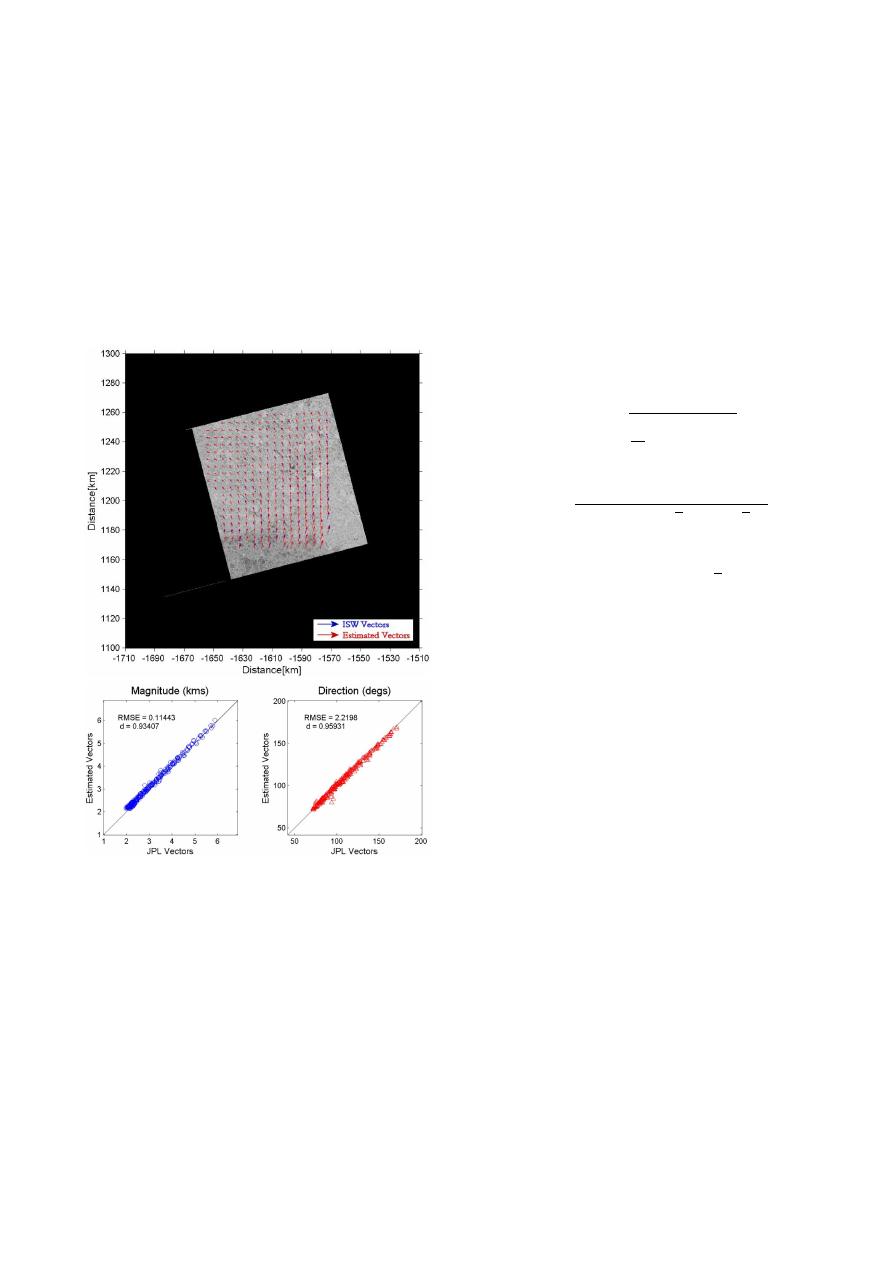
Section 3.2. The global motion field used in the comparison
in comparison with the ISW vectors. The estimated mo-
is obtained by converting the motion field from pixel coor-
tion field in the images below have been computed using
a 3232 window and then overlaid, using linear interpola-
dinates to the Special Sensor Microwave Imager (SSM/I)
grid coordinates and plotting them in tandem with the ISW
tion, on a 5 km SSM/I grid for comparison with the ISW
motion vectors.
vectors. Scatter plots show the magnitude and phase vari-
ation between our estimates and the ISW vectors for the
To maximize the throughput of the FFT modules the
spatially collocated positions.
phase correlation is performed on a window size with pow-
Figure 1 is an illustrative example of the comparison be-
ers of 2. Depending on the spatial resolution required for
tween the ISW ground truth vectors (in blue) and the esti-
the interpolation of the motion field, the block size can be
adjusted at 88, 1616 or 3232 leading to an output mo-
mated vectors (in red). The bottom panel in Figure 1 shows
scatter plots of the magnitude and directional components
tion field at 0.8 km, 1.6 km or 3.2 km resolution.
of the estimated vectors with the ISW vectors.
Two statistical measures of the similarity, the Root Mean
Square Error (Eq. 2) and the index of agreement (Eq. 3)
have been computed.
1
kK
(pk - ok )2
RM SE =
(2)
K
=1
K
ωk (pk - ok )γ
k=1
dγ = 1 -
K
(3)
γ
k=1 ωk (|pk - o| + |ok - o|)
where pk are the predicted samples, ok are the observed
ground truth vectors, wk are the weight functions which
are assumed uniform for this study and o is the mean of
the observed data. γ is the order of index and according to
Willmott [43], γ = 1 is most robust for comparing results
because of its linear approach to a perfect match.
Analysis of the image pairs using higher resolution
analysis windows (Figure 2) reveals precise demarcations
corresponding to the regions in the ice-flow undergoing sig-
nificant amounts of non-rigid dynamics. Based on the vari-
ance of the magnitude and direction of the motion field, the
cluster map as shown in Figure 2 was created using a quad-
tree model.
This result reveals the usefulness of local higher order
motion in the vicinity of the regions of discontinuity. Given
the global motion compensated images, local non-rigid dy-
namics was first extracted using the simplest model of the
local motion. Under the assumption that magnitude of the
differential motion is small, a piecewise linear approxima-
tion of the non rigid motion using phase correlation was
Figure 1. Comparison of motion vectors from
applied. As seen in Figure 3, the estimated local motion
the ERS-1 image pair at orbit 3402 frame 5103
vectors are overlaid upon the correlation map to verify the
and orbit 3412 frame 5693 shown with our
goodness-of-fit as are the ISW vectors in validation. Exper-
estimated vectors (red) and the ISW vectors
imentally, a threshold correlation of < 0.2 is found to be the
(blue). Scatter plot comparisons of the mag-
most appropriate for demarcating between continuous and
nitude and phase between these two data sets
discontinuous regimes. This low correlation corresponds to
shown in accompanying panels.
regions where the magnitude of deformation far exceeds the
piece-wise approximation.
The dynamic region analyzed and described earlier in
The subsequent results in Figure 1 show the accuracy of
(Figure 2) is shown again in Figure 4 in the same format
the estimates obtained by the phase correlation technique
as Figure 3 for comparison. This dynamic region contains





 Previous Page
Previous Page
