(= 273.15 kelvins or 0C) computes from the Clausius
cal definitions and relationships used in this study. Liq-
uid inclusions occur as veins along three-grain bound-
Clapeyron equation as
aries, as nodes where four veins join, and as lenses be-
T p - p0 pi - po
tween two-grain boundaries. Veins dilate to widths of
∆T = 0 l
-
- KF C
tenths of millimeters as ice nears 0C, and thus, together
(1)
ρi
Lil pl
with nodes, form a permeable network for the flow of
water. Nye (1989) provides a detailed description of
where Lil is the latent heat of freezing (3.335 105J
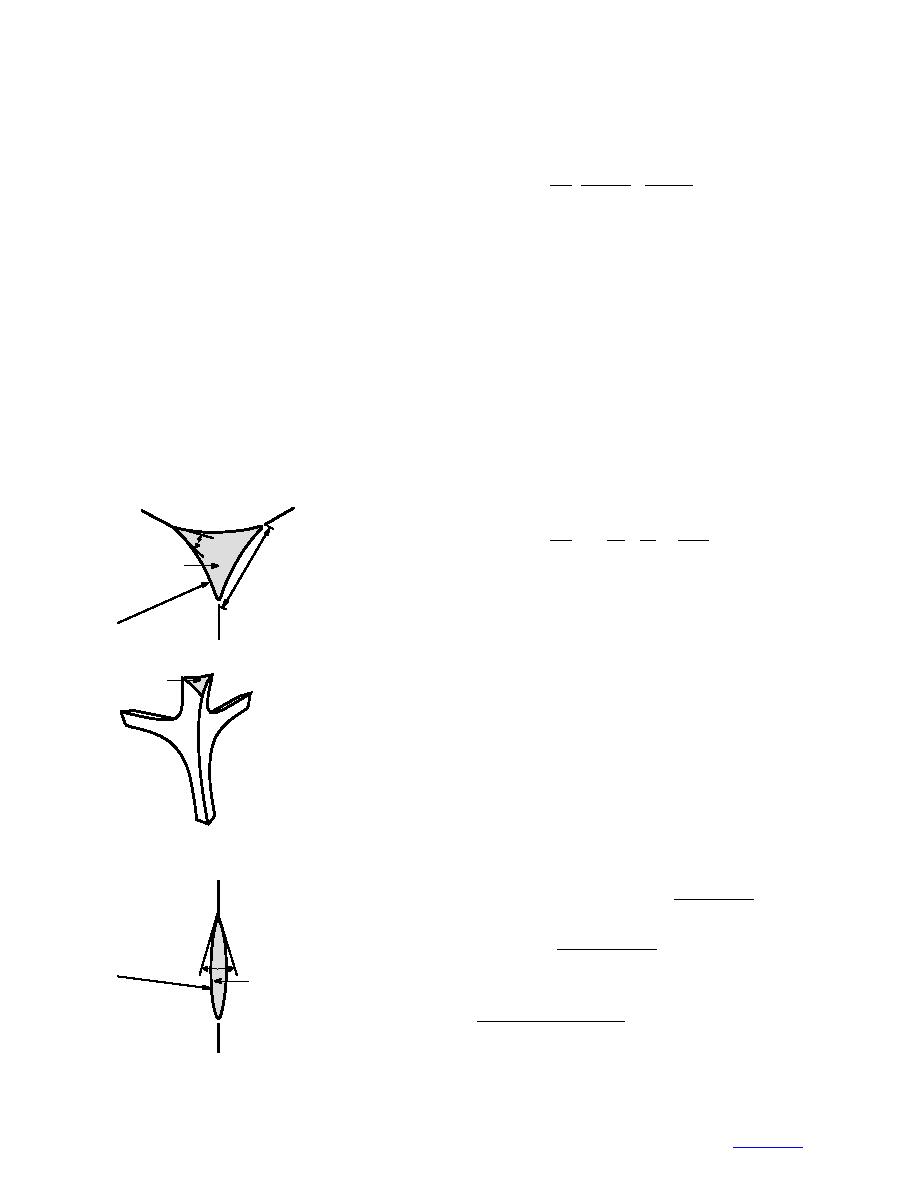
the geometry of the veinnode system. Veins have a
kg1), p0 is the reference pressure (atmospheric), pl is
concave triangular cross section (Fig. 5a) which is fixed
the water pressure, pi is the ice pressure, ρl is the den-
by the dihedral angle and does not vary with vein size.
sity of water (1000 kg m3), ρi is the density of ice
Nodes take the shape of tetrahedrons with nonspherical
(917 kg m3), C is the molality of the liquid water in-
faces and open corners (Fig. 5b). Water lenses form
clusion (moles kg1), and KF is the modal freezing point
spherical caps (Fig. 5c), where divergence at the ice
depression constant for water (= 1.855 K kg mole1).
waterice juncture is again fixed by the dihedral angle.
Thus, increases or decreases in the pressure of ice or
Because of the respective concave and convex shapes
water, respectively, lower the equilibrium temperature.
of the ice/water interfaces, water is under tension in
The Laplace equation defines the pressure drop across
veins and under pressure in lenses.
the ice/water interface as pi pl = 2σil/r il, where r il is
The phase-equilibrium temperature of water inclu-
the mean radius of curvature of the interface and σil its
sions is defined by pressures in the ice and liquid phases
surface tension (0.034 J m2). Taking the excess pres-
and by impurities in the water. The change in equilib-
sure in the ice as the gauge pressure, pG, and defining
rium temperature ∆T from its bulk melt value T0
pl by the Laplace equation, eq 1 becomes:
Ice
1 2σ il
1
T0
- KF C.
∆T =
- -
pG
(2)
φ
ρl ρi ρlril
Lil
Water
dv
The terms in eq 2 represent, respectively, temperature
rv
depression due to increased gauge or "atmospheric"
pressure, interfacial curvature, and impurities. We as-
a. Vein cross section.
sume that the gauge pressure acts equilaterally in the
ice, but note that this is not necessarily the case.
The molality Cv of the veinnode system computes
Ice
Water
as mv/vv, where mv is the vein bulk molality and vv is
the fractional volume of liquid. Applying thermody-
namic reasoning, Nye (1989) computes the ratio of liq-
uid volume in nodes to that in veins as 13.89dv/G. The
fractional volume of liquid in the veinnode system is
then Avl (1 + 6.719rv/G), where Av is the cross-sectional
area of a vein and l the vein length per unit ice volume.
b. Perspective drawing of
Using the geometric relationships in Table 1, eq 2, and
node. (After Nye 1989.)
the Laplace equation, the equilibrium temperature for
veins is (Lliboutry 1996, Mader 1992b*)
2.785 10 -8
∆Tv = -7.413 10 -8 pG -
rv
Ice
8.528 G3 mv
- 2
(3)
rv (G + 6.719rv )
φ
rL
Water
where rv is the radius of curvature of the vein. Figure 6
* In deriving eq 3, we do not include pumping of solutes by freeze
c. Lens cross section.
thaw contraction and expansion of the ice volume. This and smaller
grain sizes for our samples yield smaller vein widths than observed
Figure 5. Geometry of water inclusions in ice.
by Mader (1992b).
5





 Previous Page
Previous Page
