80
140
70
120
60
100
50
80
40
60
30
net AFDD
40
20
Average Daily
20
10
Air T (f)
0
0
Days
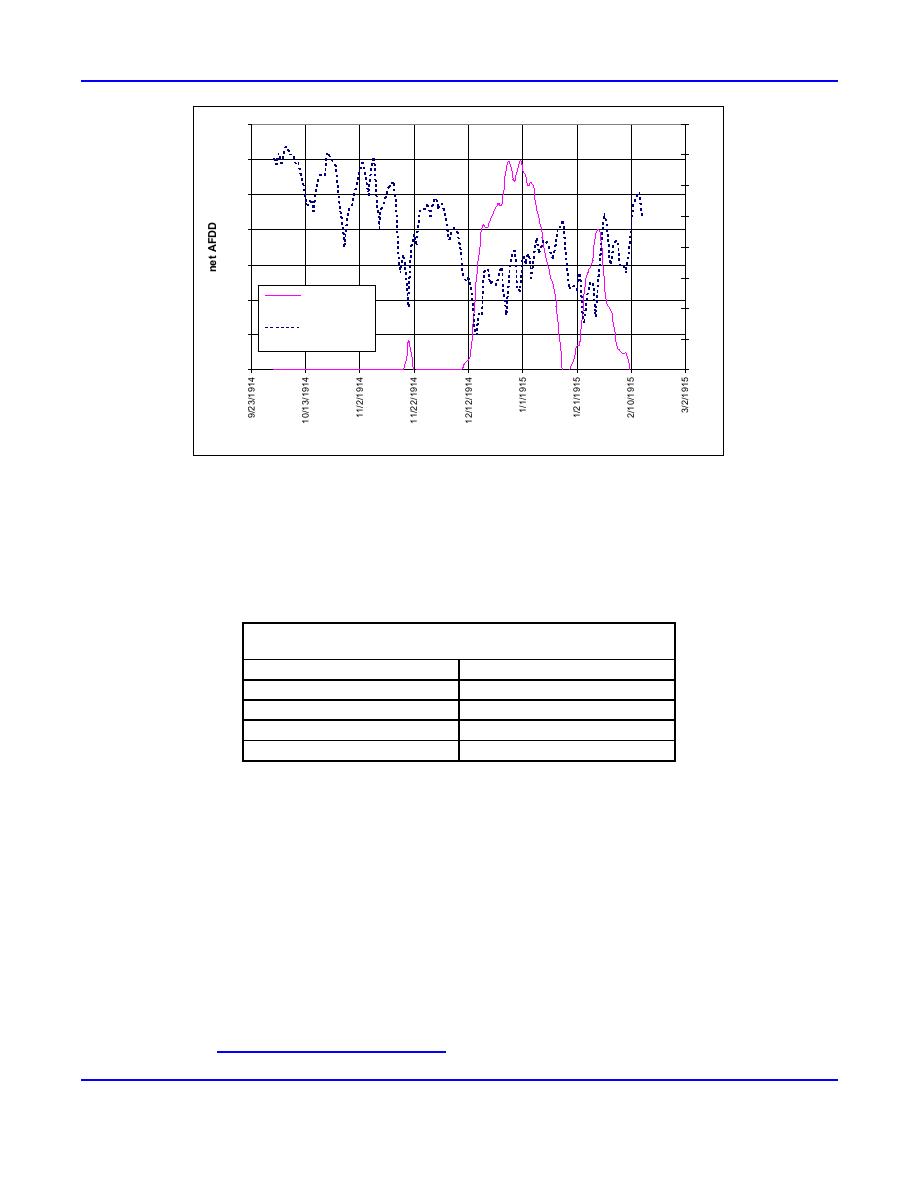
Figure 4. Example of average daily air temperature and net AFDD (Cairo, Illinois, WY 1915).
Ice thickness in inches is then estimated using the modified Stefan equation presented in USACE (2002):
ti = C (AFDD)0.5
(2)
where C is a coefficient, usually ranging between 0.3 and 0.6 and AFDD is in F days (Table 1).
Table 1. Coefficient for use in modified Stefan equation with ice
thickness in inches, AFDD in F days (from USACE 2002).
Condition
Typical value of C
Windy lake with no snow
0.8
Average lake with snow
0.5 to 0.7
Average river with snow
0.12 to 0.15
Sheltered small river
0.21 to 0.41
Using equation 2 with a coefficient of 0.6, we would predict that 300 AFDD would produce a 10-inch-thick sheet ice
cover. Snow cover on top of the ice can insulate it, decreasing heat transfer and effectively lowering the coefficient used in
equation 2. If ice cover growth is affected by underturning, shoving, or frazil deposition, the coefficient in equation 2 should
be increased. Once the peak annual AFDD is reached and thawing days exceed freezing days, the coefficients shown in Table
1 are no longer applicable for equation 2. Ice thinning processes result from changes in the air and water thermal regimes and
in the ice cover itself. Although some research (e.g., Bilello 1980) has indicated that a different set of coefficients could be
used to describe thinning of the ice based on meteorological conditions, a complete examination of the problem has not been
conducted to date. Thus, no coefficients are suggested for estimating ice thickness after the peak AFDD.
Process Used to Estimate Ice Thickness Based on Meteorological Data
In general, the process used to estimate ice thickness from thermally induced growth as discussed above is as follows:
1. Locate the National Weather Service (NWS) meteorological station closest to the site with the longest and most
reliable period of record. Stations can be identified from lists available at the National Climatic Data Center
(NCDC, http://lwf.ncdc.noaa.gov/oa/ncdc.html). Generally, first-order stations, which are usually fully instru-
mented and therefore record a complete range of meteorological variables, are preferred over cooperative
ERDC/CRREL TN-04-3
3





 Previous Page
Previous Page
