A as our lower bounding cost, we can not be certain that this is the greatest lower
bound. If the application of the branch-and-bound method finds feasible solutions
with costs lower than our solution found by method A, then we must from that point
on use the unconstrained discrete solution as the greatest lower bound.
Note that, similar to method A (Fig. 9), method B (Fig. 10) would also provide a
number of pipe segments whose diameters are continuous as a result of the
refinement process used. Thus, we would proceed in the same manner with the
branch-and-bound method regardless of which of the two methods had been used
for the pipe size refinement process.
The application of the branch-and-bound method to our feasible solution of
method A or B is straightforward and proceeds as described earlier. Many of the
branches will have infeasible designs, since we know decreasing any of the continu-
ous pipe diameters will result in the violation of at least one constraint, unless other
pipe diameters have also been increased. Thus, any branch that only decreases pipe
diameters in any one of the combinations in which they appear in the previously
violated constraints will be infeasible and need not be explored.
Consider a hypothetical case where we have four pipe segments with continuous
diameters after the application of either method A or B. If we limit ourselves to only
the two discrete pipe sizes that bracket the continuous values found, we will have
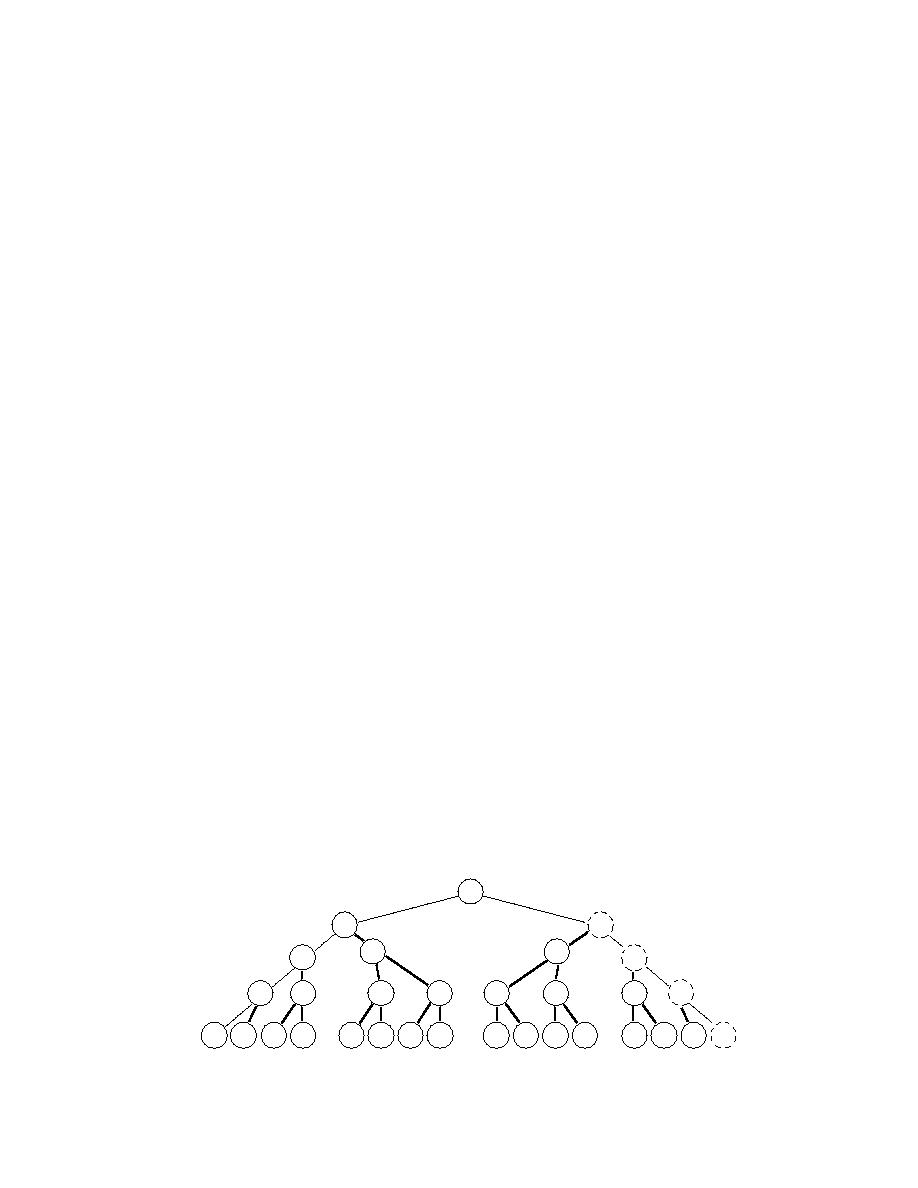
24 = 16 possible discrete solutions. A "tree" diagram of the problem is shown in
Figure 13. The symbols within each "node" of the tree represent the particular case
being evaluated. The "0" symbol indicates the continuous pipe size as found by
either method A or B. A "+" symbol indicates the next larger discrete pipe size and
a "" symbol indicates the next smaller discrete pipe size. The sequence of the
symbols represents the order of the four pipe segments under investigation. As
noted above, any possibilities that only decrease the size of one or more pipe
segments are immediately known to be infeasible. These nodes have been shown
with dotted outlines in Figure 13.
Applying the branch-and-bound method, we would proceed initially by choos-
ing the first pipe segment to branch on. Starting at the top of Figure 13, we branch
on the first pipe segment by computing the value of the objective function with the
branching diameter, rounded both up and down to the adjacent discrete diameter
values. However, we notice that one of the options, the ( 000) case, is infeasible.
Thus, there is no use in computing the value of the objective at that point since it's
of no use as a lower bound on the constrained problem. In this case we then proceed
further down this branch in search of a feasible case. Suppose that we find that the
( + + 0) is the first feasible case in this branch. We then branch on the last pipe
segment by examining the cases ( + + +) and ( + + ). Assume that we find both of
these to be feasible, but the ( + + ) case is lower in cost. This is our first completely
discrete and feasible design. It now becomes our upper bounding cost. If this cost is
sufficiently close to our current lower bounding cost of the (0000) case, then we can
(0000)
(+000)
(-000)
(+-00)
(-+00)
(++00)
(--00)
(--+0)
(---0)
(+++0)
(++-0)
(+-+0)
(+--0)
(-++0)
(-+-0)
(++++) (++++) (++-+)
(++--)
(-+++)
(-++-)
(-+--)
(--++)
(--+-)
(---+)
(----)
(+-++)
(+-+-)
(+--+)
(+---)
(-+-+)
Figure 13. Hypothetical branch-and-bound problem.
60





 Previous Page
Previous Page
